(本小题满分12分)
某商品每件成本9元,售价为30元,每星期卖出432件,如果降低价格,销售量可以增加,且每星期多卖出商品件数与商品单价的降低值x (单位:元,0≤x≤30)的平方成正比,已知商品单价降低2元时,一星期多卖出24件。
(1)将一个星期的商品销售利润表示成x的函数 ;
;
(2)如何定价才能使一个星期的商品销售利润最大?
已知数列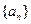 的前
的前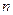 项和为
项和为 ,且
,且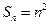 .数列
.数列 为等比数列,且
为等比数列,且 ,
,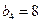 .
.
(Ⅰ)求数列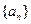 ,
, 的通项公式;
的通项公式;
(Ⅱ)若数列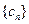 满足
满足 ,求数列
,求数列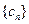 的前
的前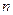 项和
项和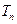 ;
;
已知函数 ,
,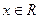
(1)求函数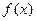 的最小正周期;
的最小正周期;
(2)记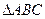 的内角A,B,C的对边长分别为
的内角A,B,C的对边长分别为 ,若
,若 ,求
,求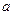 的值。
的值。
某班从6名干部中(其中男生4人,女生2人),选3人参加学校的义务劳动。
(1)设所选3人中女生人数ξ,求ξ的分布列及数学期望;
(2)求男生甲或女生乙被选中的概率;
(3)在男生甲被选中的情况下,求女生乙也被选中的概率。
如图,四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=CD,E是PC的中点。
(1)证明PA平面BDE;
(2)求二面角B-DE-C的平面角的余弦值;
(3)在棱PB上是否存在点F,使PB⊥平面DEF?
证明你的结论。