(本小题满分12分)
某校高三数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示.若130~140分数段的人数为2人.
(Ⅰ)估计这所学校成绩在90~140分之间学生的参赛人数;
(Ⅱ)现根据初赛成绩从第一组和第五组(从低分段到高分段依次为第一组、第二组、…、第五组)中任意选出两人,形成帮扶学习小组.若选出的两人成绩之差大于20,则称这两人为“黄金搭档组”,试求选出的两人为“黄金搭档组”的概率.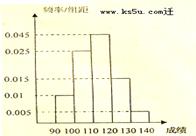
在直角坐标系
中,以坐标原点为极点,
轴正半轴为极轴建立极坐标系,半圆
的极坐标方程为
.
(1)求
得参数方程;
(2)设点
在
上,
在
处的切线与直线
垂直,根据(1)中你得到的参数方程,确定
的坐标.
如图,
是
外一点,
是切线,
为切点,割线
与
相交于
,
,
为
的中点,
的延长线交
于点
.证明:
(1)
;
(2)
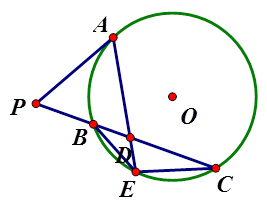
已知函数
,曲线
在点
处的切线与 轴交点的横坐标为
.
轴交点的横坐标为
.
(1)求
;
(2)证明:当
时,曲线
与直线
只有一个交点.
设
分别是椭圆
的左右焦点,
是
上一点且
与
轴垂直,直线
与
的另一个交点为
.
(1)若直线
的斜率为
,求
的离心率;
(2)若直线
在
轴上的截距为
,且
,求
.
某市为了考核甲、乙两部门的工作情况,随机访问了50位市民,根据这50位市民对这两部门的评分(评分越高表明市民的评价越高),绘制茎叶图如下:
(1)分别估计该市的市民对甲、乙两部门评分的中位数;
(2)分别估计该市的市民对甲、乙两部门的评分高于90的概率;
(3)根据茎叶图分析该市的市民对甲、乙两部门的评优.