(本题满分14分)
已知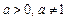 ,设P:函数
,设P:函数 内单调递减;Q:二次函数
内单调递减;Q:二次函数 的图象与
的图象与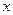 轴交于不同的两点. 如果P与Q有且只有一个正确,求
轴交于不同的两点. 如果P与Q有且只有一个正确,求 的取值范围.
的取值范围.
已知 ,
, 是平面上的两个定点,动点
是平面上的两个定点,动点 满足
满足 .
.
(1)求动点 的轨迹方程;
的轨迹方程;
(2)已知圆方程为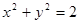 ,过圆上任意一点作圆的切线,切线与(1)中的轨迹交于
,过圆上任意一点作圆的切线,切线与(1)中的轨迹交于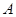 ,
, 两点,
两点, 为坐标原点,设
为坐标原点,设 为
为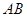 的中点,求
的中点,求 长度的取值范围.
长度的取值范围.
已知数列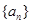 ,
,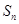 是其前
是其前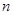 项的且满足
项的且满足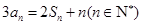
(1)求证:数列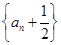 为等比数列;
为等比数列;
(2)记 ,求
,求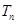 的表达式。
的表达式。
设函数 ,其中向量
,其中向量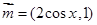 ,
,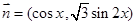 ,
,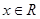 .
.
(1)求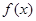 的最小正周期与单调递减区间;
的最小正周期与单调递减区间;
(2)在△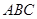 中,
中,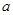 、
、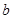 、
、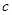 分别是角
分别是角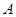 、
、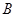 、
、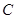 的对边,已知
的对边,已知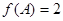 ,
,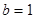 ,△
,△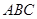 的面积为
的面积为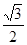 ,求
,求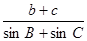 的值.
的值.
已知圆C: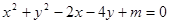 。
。
(1)求m的取值范围。
(2)当m=4时,若圆C与直线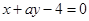 交于M,N两点,且
交于M,N两点,且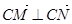 ,求
,求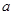 的值。
的值。
(本小题满分14分)已知椭圆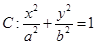 (
(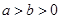 )的左、右顶点分别为
)的左、右顶点分别为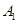 ,
,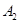 ,
,
且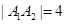 ,
,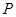 为椭圆上异于
为椭圆上异于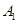 ,
,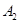 的点,
的点,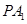 和
和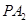 的斜率之积为
的斜率之积为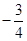 .
.
(1)求椭圆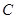 的标准方程;
的标准方程;
(2)设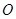 为椭圆中心,
为椭圆中心,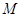 ,
,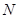 是椭圆上异于顶点的两个动点,求
是椭圆上异于顶点的两个动点,求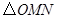 面积的最大值.
面积的最大值.