已知各项均为正数的数列{an}满足2a2n+1+3an+1an-2a2n=0(n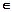
 )且a3+
)且a3+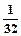 是a2,a4的等差中项,数列{bn}的前n项和Sn=n2
是a2,a4的等差中项,数列{bn}的前n项和Sn=n2
(1)求数列{an}与{bn}的通项公式;
(2)若Tn= ,求证:Tn<
,求证:Tn<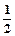
(3)若cn=-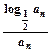 ,T/n=c1+c2+…+cn,求使T/n+n
,T/n=c1+c2+…+cn,求使T/n+n 2n+1>125成立的正整数n的最小值
2n+1>125成立的正整数n的最小值
如图,四面体ABCD中,O、E分别是BD、BC的中点
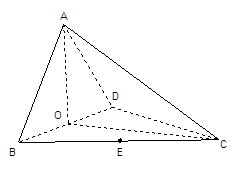
(I)求证: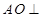 平面BCD;
平面BCD;
(II)求异面直线AB与CD所成角的余弦值;
(III)求点E到平面ACD的距离。
设函数 (1)设
(1)设 的内角,且为钝角,求
的内角,且为钝角,求 的最小值;
的最小值;
(2)设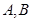 是锐角
是锐角 的内角,且
的内角,且 求
求 的三个内角的大小和AC边的长。
的三个内角的大小和AC边的长。
一个多面体的直观图和三视图如下:(其中 分别是
分别是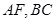 中点)
中点)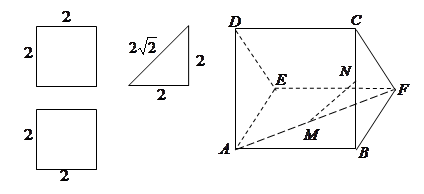
(1)求证: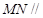 平面
平面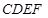 ;
;
(2)求多面体 的体积.
的体积.
如图,已知正方形ABCD的边长为1,FD⊥平面ABCD,EB⊥平面ABCD,FD=BE=1,M为BC边上的动点.
(1)设N为EF上一点,当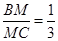 时,有DN ∥平面AEM,求
时,有DN ∥平面AEM,求 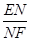 的值;
的值;
(2)试探究点M的位置,使平面AME⊥平面AEF。
如图,长方体AC1中,AB=2,BC=AA1=1.E、F、G分别为棱DD1、D1C1、BC的中点.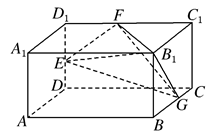
(1)求证:平面 平面
平面 ;
;
(2)在底面A1D1上有一个靠近D1的四等分点H,求证: EH∥平面FGB1;
(3)求四面体EFGB1的体积.