(本小题满分12分)
已知函数f(x)=2sinωx·cos(ωx+)+(ω>0)的最小正周期为4π.
(1)求正实数ω的值;
(2)在△ABC中,内角A、B、C的对边分别为a、b、c,且满足2bcosA=acosC+ccosA,求f(A)的值.
定义区间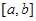 的区间长度为
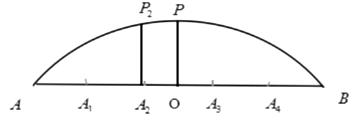
的区间长度为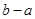 ,如图是某圆拱形桥一孔圆拱的示意图.这个圆的圆拱跨度
,如图是某圆拱形桥一孔圆拱的示意图.这个圆的圆拱跨度 ,拱高
,拱高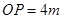 ,建造时每间隔
,建造时每间隔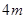 需要用一根支柱支撑,求支柱
需要用一根支柱支撑,求支柱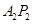 的高度所处的区间
的高度所处的区间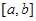 .(要求区间长度为
.(要求区间长度为 )
)
己知圆心为 的圆经过点
的圆经过点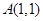 和
和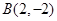 ,且圆心
,且圆心 在直线
在直线 上,求圆心为
上,求圆心为 的圆的标准方程.
的圆的标准方程.
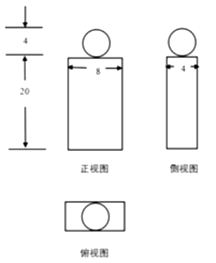
己知一几何体的三视图,试根据三视图计算出它的表面积和体积(结果保留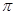 )
)
(本小题满分16分)设常数 ,函数
,函数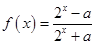 .
.
(1)当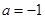 时,判断并证明函数
时,判断并证明函数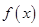 在
在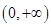 的单调性;
的单调性;
(2)若函数 的是奇函数,求实数a的值;
的是奇函数,求实数a的值;
(3)当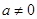 时,若存在区间
时,若存在区间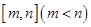 ,使得函数
,使得函数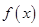 在
在 的值域为
的值域为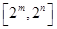 ,求实数
,求实数 的取值范围.
的取值范围.
(本小题满分16分)已知二次函数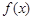 满足
满足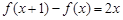 且
且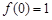 .
.
(1)求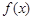 的解析式;
的解析式;
(2)当 时,不等式:
时,不等式: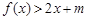 恒成立,求实数
恒成立,求实数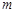 的范围.
的范围.
(3)设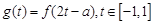
 ,求
,求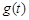 的最大值;
的最大值;