(本小题满分13分)
设函数y=f(x)的定义域为(0,+∞),且在(0,+∞)上单调递增,若对任意x,y∈(0,+∞)都有:f(xy)=f(x)+f(y)成立,数列{an}满足:a1=f(1)+1,f(-)+f(+)=0.设Sn=aa+aa+aa+…+aa+aa.
(1)求数列{an}的通项公式,并求Sn关于n的表达式;
(2)设函数g(x)对任意x、y都有:g(x+y)=g(x)+g(y)+2xy,若g(1)=1,正项数列{bn}满足:b=g(),Tn为数列{bn}的前n项和,试比较4Sn与Tn的大小.
已知O为坐标原点,△AOB中,边OA所在的直线方程是 ,边AB所在的直
,边AB所在的直
线方程是 ,且顶点B的横坐标为6。
,且顶点B的横坐标为6。
(1)求△AOB中,与边AB平行的中位线所在直线的方程;
(2)求△AOB的面积;
(3)已知OB上有点D,满足△AOD与△ABD的面积比为2,求AD所在的直线方程。
(本小题满分14分)
已知方程 ,
,
(1)若此方程表示圆,求 的取值范围;
的取值范围;
(2)若(1)中的圆与直线 相交于
相交于 、
、 两点,且
两点,且 (
( 为坐标原点),求
为坐标原点),求 的值;
的值;
(3)在(2)的条件下,求以 为直径的圆的方程。
为直径的圆的方程。
(本小题满分13分)
已知圆 和直线
和直线 ,
,
(1)求证:不论 取什么值,直线和圆总相交;
取什么值,直线和圆总相交;
(2)求 取何值时,直线被圆截得的弦最短,并求出最短弦的长;
取何值时,直线被圆截得的弦最短,并求出最短弦的长;
(本小题满分13分)
如图,在四棱锥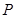 -
- 中,底面
中,底面 是边长为
是边长为 的正方形,
的正方形,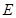 、
、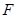 分别为
分别为 、
、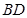 的中点,侧面
的中点,侧面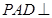 底面
底面 ,且
,且 。
。
(Ⅰ)求证: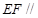 平面
平面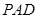 ;
;
(Ⅱ)求证:平面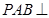 平面
平面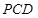 ;
;
(Ⅲ)求三棱锥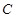 -
-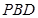 的体积。
的体积。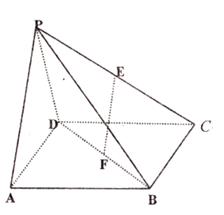
(本小题满分14分)
已知点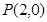 ,及⊙
,及⊙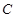 :
: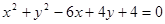 。
。
(Ⅰ)当直线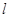 过点
过点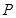 且与圆心
且与圆心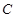 的距离为1时,求直线
的距离为1时,求直线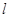 的方程;
的方程;
(Ⅱ)设过点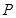 的直线与⊙
的直线与⊙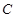 交于
交于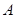 、
、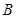 两点,当
两点,当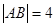 ,求以线段
,求以线段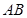 为直径的圆的方程。
为直径的圆的方程。