(满分14分) 是首项
是首项 的等比数列,且
的等比数列,且 ,
, ,
, 成等差数列,
成等差数列,
(1)求数列 的通项公式;
的通项公式;
(2)若 ,设
,设 为数列
为数列 的前
的前 项和,若
项和,若 ≤
≤ 对一切
对一切 恒成立,求实数
恒成立,求实数 的最小值.
的最小值.
(本小题满分13分)
已知函数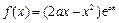 ,其中a为常数,且
,其中a为常数,且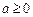 .
.
(Ⅰ)若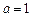 ,求函数
,求函数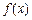 的极值点;
的极值点;
(Ⅱ)若函数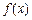 在区间
在区间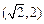 上单调递减,求实数a的取值范围.
上单调递减,求实数a的取值范围.
(本小题满分13分)
为保护水资源,宣传节约用水,某校4名志愿者准备去附近的甲、乙、丙三家公园进行宣传活动,每名志愿者都可以从三家公园中随机选择一家,且每人的选择相互独立.
(Ⅰ)求4人恰好选择了同一家公园的概率;
(Ⅱ)设选择甲公园的志愿者的人数为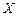 ,试求
,试求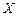 的分布列及期望.
的分布列及期望.
(本小题满分14分)
已知四棱锥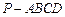 ,底面
,底面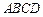 为矩形,侧棱
为矩形,侧棱 ,其中
,其中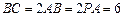 ,
,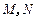 为侧棱
为侧棱 上的两个三等分点,如图所示.
上的两个三等分点,如图所示.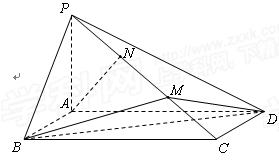
(Ⅰ)求证: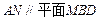 ;
;
(Ⅱ)求异面直线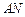 与
与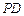 所成角的余弦值;
所成角的余弦值;
(Ⅲ)求二面角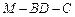 的余弦值.
的余弦值.
(本小题满分13分)
记等差数列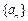 的前n项和为
的前n项和为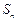 ,已知
,已知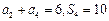 .
.
(Ⅰ)求数列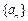 的通项公式;
的通项公式;
(Ⅱ)令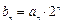
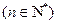 ,求数列
,求数列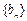 的前n项和
的前n项和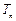 .
.
已知数列{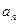 }中,
}中,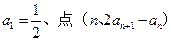 在直线y=x上,其中n=1,2,3….
在直线y=x上,其中n=1,2,3….
(Ⅰ)令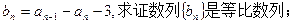
(Ⅱ)求数列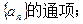
(Ⅲ)设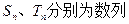
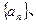
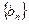 的前n项和,是否存在实数
的前n项和,是否存在实数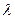 ,使得数列
,使得数列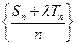 为等差数列?若存在,试求出
为等差数列?若存在,试求出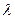 .若不存在,则说明理由。
.若不存在,则说明理由。