(本题满分15分) 已知实数a满足1＜a≤2，设函数f (x)＝
x3－
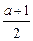x2＋ax．
(Ⅰ) 当a＝2时，求f (x)的极小值；
(Ⅱ) 若函数g(x)＝4x3＋3bx2－6(b＋2)x (b∈R) 的极小值点与f (x)的极小值点相同，
求证：g(x)的极大值小于等于10．
（本题10分）
某医院用50万元购买了一台医疗仪器，这台仪器启用后每天都要进行保养、维修，设备在启用以后的第n（n∈N*）天应付保养维修费为（n+99）元。
（1） 若使用100天后报废 ，每天的平均
消耗是多少？
（2）使用多少天报废能使平均每天的耗费最少？
（本题9分）
已知椭圆C经过点M（1，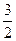
），两个焦
点为（－1，0）、（1，0）。
（1）求椭圆C的方程；
（2）直线y=2x－1与椭圆C相交于A、B两点，求线段AB的长。
（本题9分）
在空间四边形ABCD中，CB=CD，AD⊥BD，点E、F分别是AB，BD的中点。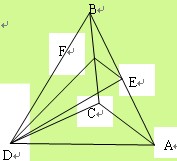
求证：
（1）直线EF∥平面ACD；
（2）平面EFC⊥平面BCD。
（本题9分）
已知函数f(x)=2cosx(sinx－cosx)+1。
（1）求函数f(x)的最小值以及取最小值时x的取值；
（2）求函数f(x)的单调递增区间。
（本题9分）
已知等差数列﹛an﹜满足：a3=1
5， a5+a7=18。
（1）求数列﹛an﹜的通项an；
（2）设﹛bn－an﹜是首项为1，公比为3的等比数列，求数列﹛bn﹜的通项公式和前n项和Sn。