(本小题满分12分)如图在三棱锥P-ABC中,PA=3,AC=AB=4,PB=PC=BC=5,D、E分别是BC、AC的中点,F为PC上的一点,且PF:FC=3:1。
(Ⅰ)求证: ;
;
(Ⅱ)试在PC上确定一点G,使平面ABG//平面DEF;
(Ⅲ)在满足(Ⅱ)的情况下,求直线GB与平面ABC所成角的正弦值。
(本题满分10分) 如图,在平行四边形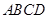 中,
中,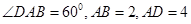 ,将
,将 沿
沿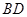 折起到
折起到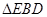 的位置,使平面
的位置,使平面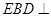 平面
平面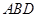 .
.
(1)求二面角E-AB-D的大小;
(2)求四面体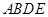 的表面积和体积.
的表面积和体积.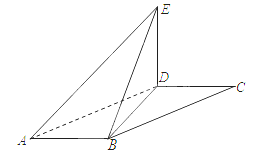
在长方体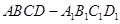 中,
中,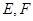 分别是
分别是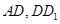 的中点,
的中点,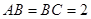 ,
,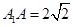 .
.
(Ⅰ)求证: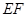 //平面
//平面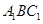 ;
;
(Ⅱ)在线段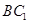 上是否存在点
上是否存在点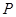 ,使直线
,使直线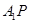 与
与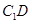 垂直,
垂直,
如果存在,求线段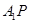 的长,如果不存在,请说明理由.
的长,如果不存在,请说明理由.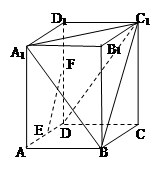
已知顶点在原点,焦点在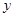 轴上的抛物线过点
轴上的抛物线过点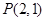 .
.
(1)求抛物线的标准方程;
(2)过点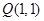 作直线交抛物线于
作直线交抛物线于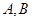 两点,使得
两点,使得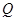 恰好平分线段
恰好平分线段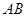 ,求直线
,求直线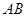 的方程
的方程
(本小题满分16分)
已知 (
(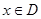 ,
,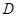 为此函数的定义域)同时满足下列两个条件:①函数
为此函数的定义域)同时满足下列两个条件:①函数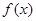
在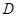 内单调递增或单调递减;②如果存在区间
内单调递增或单调递减;②如果存在区间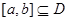 ,使函数
,使函数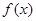 在区间
在区间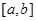 上的值域为
上的值域为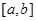 ,那么称
,那么称 ,
,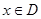 为闭函数。请解答以下问题:
为闭函数。请解答以下问题:
(1)判断函数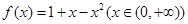 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(2)求证:函数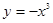 (
(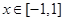 )为闭函数;
)为闭函数;
(3)若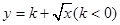 是闭函数,求实数
是闭函数,求实数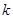 的取值范围.
的取值范围.
(本小题满分14分)
已知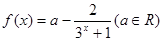 :
:
(1)用定义法证明函数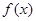 是
是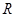 上的增函数;
上的增函数;
(2)是否存在实数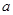 使函数
使函数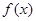 为奇函数?若存在,请求出
为奇函数?若存在,请求出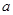 的值,若不存在,说明理由.
的值,若不存在,说明理由.