(本小题满分12分)已知函数 ,
, .
.
(1)若函数 是单调递增函数,求实数
是单调递增函数,求实数 的取值范围;
的取值范围;
(2)当 时,两曲线
时,两曲线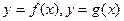 有公共点P,设曲线
有公共点P,设曲线 在P处的切线分别为
在P处的切线分别为 ,若切线
,若切线 与
与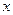 轴围成一个等腰三角形,求P点坐标和
轴围成一个等腰三角形,求P点坐标和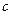 的值;
的值;
(3)当 时,讨论关于
时,讨论关于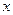 的方程
的方程 的根的个数。
的根的个数。
已知函数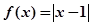 .
.
(1)用分段函数的形式表示该函数;
(2)在右边所给的坐标系中画出该函数的图象;
(3)写出该函数的定义域、值域、奇偶性、单调区间(不要求证明).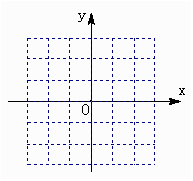
计算:
⑴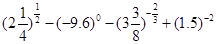 ;(2)
;(2) 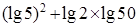
我市有甲,乙两家乒乓球俱乐部,两家设备和服务都很好,但收费方式不同.甲家每张球台每小时5元;乙家按月计费,一个月中30小时以内(含30小时)每张球台90元,超过30小时的部分每张球台每小时2元.某公司准备下个月从这两家中的一家租一张球台开展活动,其活动时间不少于15小时,也不超过40小时.(1)设在甲家租一张球台开展活动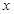 小时的收费为
小时的收费为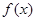 元
元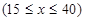 ,在乙家租一张球台开展活动
,在乙家租一张球台开展活动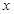 小时的收费为
小时的收费为 元
元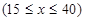 ;试求
;试求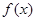 和
和 ;(2)问:选择哪家比较合算?为什么?
;(2)问:选择哪家比较合算?为什么?
某工厂今年1月、2月、3月生产某种产品的数量分别是1万件、1.2万件、1.3万件,为了估测以后每个月的产量,以 这三个月的产品数量为依据,用一个函数模拟该产品
这三个月的产品数量为依据,用一个函数模拟该产品 的月产量
的月产量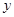 与月份
与月份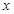 的关系,模拟的函数可以选用二次函数
的关系,模拟的函数可以选用二次函数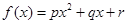 (
( 为常数,且
为常数,且 )或函数
)或函数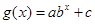 (
(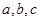 为常数,且
为常数,且 )。已知4月份该产品的产量为
)。已知4月份该产品的产量为 万件,请问用以上哪个函数作为模拟函数较好,并说明理由。
万件,请问用以上哪个函数作为模拟函数较好,并说明理由。
设二次函数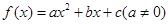 满足条件:①当
满足条件:①当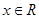 时,
时, ,且
,且 ;②
;②  在
在 上的最小值为
上的最小值为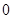 。(1)求
。(1)求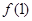 的值及
的值及 的解析式;(2)若
的解析式;(2)若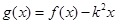 在
在 上是单调函数,求
上是单调函数,求 的取值范围;(3)求最大值
的取值范围;(3)求最大值 ,使得存在
,使得存在 ,只要
,只要 ,就有
,就有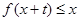 。
。