如图,已知三棱锥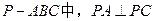 ,
,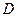 为
为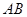 中点,
中点,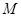 为
为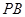 的中点,且
的中点,且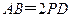 ,.
,.
(I)求证: ;
;
(II)找出三棱锥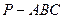 中一组面与面垂直的位置关系,并给出证明(只需找到一组即可)
中一组面与面垂直的位置关系,并给出证明(只需找到一组即可)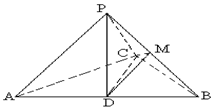
已知椭圆G: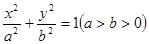 ,过点A(0,5),B(﹣8,﹣3),C、D在该椭圆上,直线CD过原点O,且在线段AB的右下侧.
,过点A(0,5),B(﹣8,﹣3),C、D在该椭圆上,直线CD过原点O,且在线段AB的右下侧.
(1)求椭圆G的方程;
(2)求四边形ABCD 的面积的最大值.
已知直线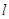 与圆C:
与圆C: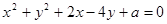 相交于A,B两点,弦AB中点为M(0,1),
相交于A,B两点,弦AB中点为M(0,1),
(1)求实数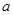 的取值范围以及直线
的取值范围以及直线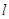 的方程;
的方程;
(2)若圆C上存在四个点到直线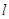 的距离为
的距离为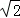 ,求实数a的取值范围;
,求实数a的取值范围;
(3)已知N(0,﹣3),若圆C上存在两个不同的点P,使 ,求实数
,求实数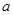 的取值范围.
的取值范围.
在平面直角坐标系中,设△ABC的顶点分别为 ,圆M是△ABC的外接圆,直线
,圆M是△ABC的外接圆,直线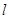 的方程是
的方程是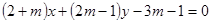 ,
,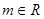
(1)求圆M的方程;
(2)证明:直线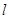 与圆M相交;
与圆M相交;
(3)若直线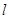 被圆M截得的弦长为3,求直线
被圆M截得的弦长为3,求直线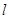 的方程.
的方程.
四棱锥P﹣ABCD中,底面ABCD是边长为8的菱形,∠BAD= ,若PA=PD=5,平面PAD⊥平面ABCD.
,若PA=PD=5,平面PAD⊥平面ABCD.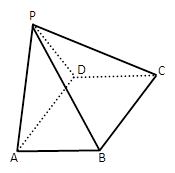
(1)求四棱锥P﹣ABCD的体积;
(2)求证:AD⊥PB.
已知 :
: ,不等式
,不等式 恒成立,
恒成立, :椭圆
:椭圆 的焦点在
的焦点在 轴上.若命题p∧q为真命题,求实数m的取值范围.
轴上.若命题p∧q为真命题,求实数m的取值范围.