如图，平面直角坐标系中有一矩形ABCD（O为原点），点A、C分别在x轴、y轴上，且C点坐标为（0,6）；将BCD沿BD折叠（D点在OC边上），使C点落在OA边的E点上，并将BAE沿BE折叠，恰好使点A落在BD的点F上.
(1)直接写出∠ABE、∠CBD的度数，并求折痕BD所在直线的函数解析式；
(2)过F点作FG⊥x轴，垂足为G，FG的中点为H，若抛物线
经过B、H、D三点，求抛物线的函数解析式；
(3)若点P是矩形内部的点，且点P在（2）中的抛物线上运动（不含B、D点），过点P作PN⊥BC分别交BC和BD于点N、M，设h=PM-MN，试求出h与P点横坐标x的函数解析式，并画出该函数的简图，分别写出使PM<NM、PM=MN、PM>MN成立的x的取值范围。
如图，在正方形ABCD中，点E、F在线段BC上，且BE=CF，连结AF、DE相交于点G，求证：EG=FG．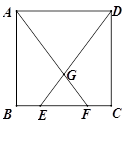
（本题满分10分，每小题5分）
（1）解分式方程：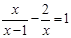
；（2）解不等式组：
．
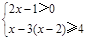如图，在平面直角坐标系xOy中，抛物线y=ax2+bx+c（a＞0）的顶点为M，直线y=m与x轴平行，且与抛物线交于点A和点B，如果△AMB为等腰直角三角形，我们把抛物线上A、B两点之间部分与线段AB围成的图形称为该抛物线的准蝶形，顶点M称为碟顶，线段AB的长称为碟宽．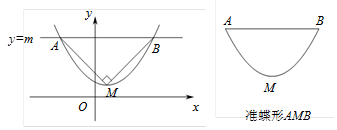
（1）抛物线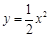
的碟宽为，抛物线y=ax2（a＞0）的碟宽为．
（2）如果抛物线y=a(x－1)2－6a（a＞0）的碟宽为6，那么a=．
（3）将抛物线yn=anx2+bnx+cn（an＞0）的准蝶形记为Fn（n=1，2，3，），我们定义F1，F2，，Fn为相似准蝶形，相应的碟宽之比即为相似比．如果Fn与Fn-1的相似比为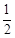
，且Fn的碟顶是Fn-1的碟宽的中点，现在将（2）中求得的抛物线记为y1，其对应的准蝶形记为F1．
①求抛物线y2的表达式；
②请判断F1，F2，，Fn的碟宽的右端点是否在一条直线上？如果是，直接写出该直线的表达式；如果不是，说明理由．
在Rt△ABC中，∠ACB=90°，D是AB的中点，DE⊥BC于E，连接CD．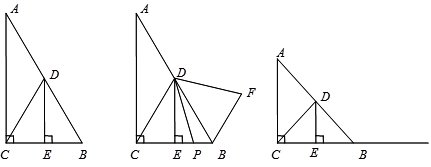
图1图2图3
（1）如图1，如果∠A=30°，那么DE与CE之间的数量关系是．
（2）如图2，在（1）的条件下，P是线段CB上一点，连接DP，将线段DP绕点D逆时针旋转60°，得到线段DF，连接BF，请猜想DE、BF、BP三者之间的数量关系，并证明你的结论．
（3）如图3，如果∠A=α（0°＜α＜90°），P是射线CB上一动点（不与B、C重合），连接DP，将线
段DP绕点D逆时针旋转2α，得到线段DF，连接BF，请直接写出DE、BF、BP三者之间的数量关系（不
需证明）．
已知：关于x的一元二次方程－x2+(m+1)x+(m+2)=0（m＞0）．
（1）求证：该方程有两个不相等的实数根；
（2）当抛物线y=－x2+(m+1)x+(m+2)经过点3，0），求该抛物线的表达式；
（3）在（2）的条件下，记抛物线y=－x2+(m+1)x+(m+2)在第一象限之间的部分为图象G，如果直线
y=k(x+1)+4与图象G有公共点，请结合函数的图象，求直线y=k(x+1)+4与y轴交点的纵坐标t的取值
范围．