直线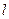 经过两条直线
经过两条直线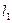 :
: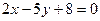 和
和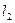
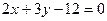 的交点,且
的交点,且 分这两条直线与
分这两条直线与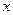 轴围成的三角形面积为
轴围成的三角形面积为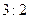 两部分,求直线
两部分,求直线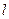 的一般式方程。
的一般式方程。
设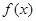 是定义在
是定义在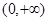 上的单调增函数,满足
上的单调增函数,满足 ,
,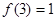 ,
,
求(1) ;
;
(2)若 ,求
,求 的取值范围。
的取值范围。
设向量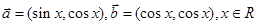 ,函数
,函数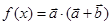 .
.
(Ⅰ)求函数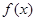 的最大值与最小正周期;
的最大值与最小正周期;
(Ⅱ)求使不等式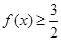 成立的
成立的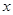 的取值范围.
的取值范围.
已知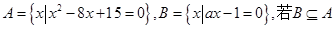 ,求实数
,求实数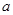 .
.
(本小题12分) 在某化学实验中,测得如下表所示的6组数据,其中x(min)表示化学反应进行的时,y(mg)表示未转化物质的量
| x(min) |
l |
2 |
3 |
4 |
5 |
6 |
| y(mg) |
39.8 |
32.2 |
25.4 |
20.3 |
16.2 |
13.3 |
(1)设x与z之问具有关系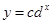 ,试根据测量数据估计c和d的值;
,试根据测量数据估计c和d的值;
(2)估计化学反应进行到10 min时未转化物质的量.
(本小题12分) 适当饮用葡萄酒可以预防心脏病,下表中的信息是19个发达国家一年中平均每人喝葡萄酒摄取酒精的升数z以及一年中每10万人因心脏病死亡的人数,
| 国家 |
澳大利亚 |
奥地利 |
比利时 |
加拿大 |
丹麦 |
芬兰 |
法国 |
冰岛 |
爰尔兰 |
意大利 |
| x |
2.5 |
3.9 |
2.9 |
2.4 |
2.9 |
0.8 |
9.1 |
0.8 |
0.7 |
7.9 |
| y |
211 |
167 |
131 |
191 |
220 |
297 |
71 |
221 |
300 |
107 |
| 国家 |
荷兰 |
新西兰 |
挪威 |
西班牙 |
瑞典 |
瑞士 |
英国 |
美国 |
德国 |
| x |
1.8 |
1.9 |
0.8 |
6.5 |
1.6 |
5.8 |
1.3 |
1.2 |
2.7 |
| y |
167 |
266 |
227 |
86 |
207 |
115 |
285 |
199 |
172 |
(1)画出散点图,说明相关关系的方向、形式及强度;
(2)求出每10万人中心脏病死亡人数,与平均每人从葡萄酒得到的酒精x(L)之间的线性回归方程.
(3)用(2)中求出的方程来预测以下两个国家的心脏病死亡率,其中一个国家的成人每年平均从葡萄酒中摄取1L的酒精,另一国则是8 L.