(本小题满分12分)
已知三棱柱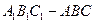 中,三个侧面均为矩形,底面
中,三个侧面均为矩形,底面 为等腰直角三角形,
为等腰直角三角形,  ,点
,点 为棱
为棱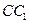 的中点,点
的中点,点 在棱
在棱 上运动.
上运动.
(1)求证

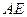 ;
;
(II)当点 运动到某一位置时,恰好使二面角
运动到某一位置时,恰好使二面角 的平面角的余弦值为
的平面角的余弦值为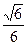 ,求点
,求点 到平面
到平面 的距离;
的距离;
(III)在(II)的条件下,试确定线段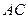 上是否存在一点
上是否存在一点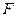 ,使得
,使得 平面
平面 ?若存在,确定其位置;若不存在,说明理由.
?若存在,确定其位置;若不存在,说明理由.
(本小题满分12 分)
分)
已知函数
(I)证明:函数 ;
;
(II)设函数 在(—1,1)上单调递增,求a的取值范围。
在(—1,1)上单调递增,求a的取值范围。
(本小题满分13分)
如图,三棱锥P—ABC中,平面PAC⊥平面BAC,AP=AB=AC=2,∠BAC=∠PAC=12 0°。
0°。
(I)求棱PB的长;
(II)求二面角P—AB—C的大小。
(本小题满分12分)
象棋比赛中,胜一局得2分,负一局得0分, 和棋一局得1分,在甲对乙的每局比赛中,甲胜、负、和的概率依次为0.5,0.3,0.2.现此二人进行两局比赛,得分累加。
和棋一局得1分,在甲对乙的每局比赛中,甲胜、负、和的概率依次为0.5,0.3,0.2.现此二人进行两局比赛,得分累加。
(I)求甲得2分的概率;
(II)记甲得 分为
分为 的分布列和期望。
的分布列和期望。
(本小题满分10分)
已知函数
(I)求函数 的最小正周期;
的最小正周期;
(I I)求函数
I)求函数 上的最大值与最小值。
上的最大值与最小值。
(本小题满分14分)
已知向量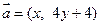 , 向量
, 向量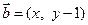 , 且
, 且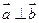 , 动点
, 动点 的轨迹为E.
的轨迹为E.
(1)求轨迹E的方程;
(2)证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B, 且 (O为坐标原点),并求出该圆的方程;
(O为坐标原点),并求出该圆的方程;