如图①，将一张矩形纸片对折，然后沿虚线剪切，得到两个（不等边）三角形纸片△ABC，△A1B1C1． 
﹙1﹚将△ABC，△A1B1C1如图②摆放，使点A1与B重合，点B1在AC边的延长线上，连接CC1交BB1于点E．求证：∠B1C1C＝∠B1BC． 
﹙2﹚若将△ABC，△A1B1C1如图③摆放，使点B1与B重合，点A1在AC边的延长线上，连接CC1交A1B于点F．试判断∠A1C1C与∠A1BC是否相等，并说明理由． 
﹙3﹚写出问题﹙2﹚中与△A1FC相似的三角形 ．
如图，在平面直角坐标系
中，
的外接圆与
轴交于点
，
，
求
的长．
（1）如图1，请你类比直线和一个圆的三种位置关系，在图1的①、②、③中，分别各画出一条直线，使它与两个圆都相离、与两个圆都相切、与一个圆相离且与另一个圆相交，并在图1的④中也画上一条直线，使它与两个圆具有不同于前面3种情况的位置关系；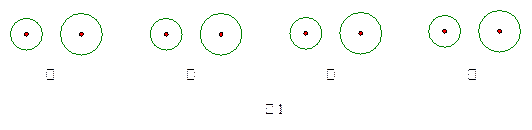
（2）如图2，点
、
在直线MN上，AB＝11厘米，
、
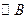的半径均为1厘米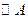．以每秒2厘米的速度自左向右运动，与此同时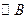，的半径
也不断增大，其半径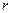
（厘米）与时间t（秒）之间的关系式为 
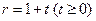．请直接写出点出发后多少秒两圆内切？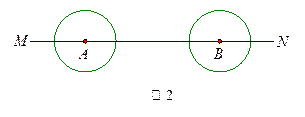
如图，
中，
、
两点在
轴的上方，点
的坐标是(-1，0)．以点为位似中心，在轴的下方作的位似图形
，并把的边长放大到原来的2倍．设点的对应点
的横坐标是2，求点的横坐标
心理学家经过调查发现，某班级的学生对概念的接受能力
与提出概念所用的时间
（单位：分）之间满足函数关系：
．其中，值越大，表示接受能力越强．
（1）第10分钟时，学生的接受能力是多少？
（2）第几分时，学生的接受能力最强？
（3）在什么范围内，学生的接受能力逐步增强？
如图，
是⊙O的直径，
是弦，
，延长到点
，使得
．
（1）求证：
是⊙O的切线；
（2）若
，求
的长