●探究   (1) 在图1中，已知线段AB，CD，其中点分别为E，F．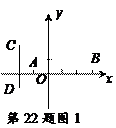

①若A (-1，0)， B (3，0)，则E点坐标为__________；
②若C (-2，2)， D (-2，-1)，则F点坐标为__________；
(2)在图2中，已知线段AB的端点坐标为A(a，b) ，B(c，d)，求出图中AB中点D的坐标（用含a，b，c，d的代数式表示），并给出求解过程．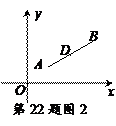

●归纳 无论线段AB处于直角坐标系中的哪个位置，当其端点坐标为A(a，b)，B(c，d)， AB中点为D(x，y) 时，x=_________，y=___________．（不必证明）
●运用 在图3中，一次函数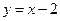与反比例函数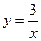的图象交点为A，B．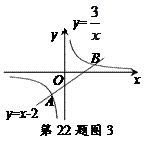

①求出交点A，B的坐标；
②若以A，O，B，P为顶点的四边形是平行四边形，请利用上面的结论求出顶点P的坐标．

科目 数学   题型 解答题   难度 中等

知识点： 四种命题及其关系