（本小题满分12分）
已知单调递增的等比数
列｛an｝满足：a2+a3+a4=28,且a3+2是a2,a4的等差中项。
（1）求数列｛an｝的通项公式;
（2）若b
n=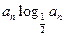
,sn=b1+b2+┉+bn,对任意正整数n,sn+(n+m)an+1<0恒成立,试求m的取值范围。
（本题12分，）有6名同学站成一排，求：
（1）甲不站排头也不站排尾有多少种不同的排法：
（2）甲、乙、丙不相邻有多少种不同的排法．（均须先列式再用数字作答）
（本题13分）在几何体ABCDE中，∠BAC=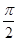 
，DC⊥平面ABC，EB⊥平面ABC，F是BC的中点，AB=AC=BE=2，CD=1．
（1）求证：DC∥平面ABE；
（2）求证：AF⊥平面BCDE；
（3）求几何体ABCDE的体积．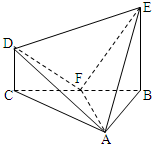
（本题12分）一只口袋内装有大小相同的5只球，其中3只白球，2只黑球．现从口袋中每次任取一球，每次取出不放回，连续取两次．问：
（1）取出的两只球都是白球的概率是多少？
（2）取出的两只球至少有一个白球的概率是多少？
（本小题满分１４分）
在医学生物学试验中，经常以果蝇作为试验对象.一个关有6只果蝇的笼子里，不慎混入了两只苍蝇（此时笼内共有8只蝇子：6只果蝇和2只苍蝇），只好把笼子打开一个小孔，让蝇子一只一只地往外飞，直到两只苍蝇都飞出，再关闭小孔.
(Ⅰ)求笼内恰好剩下1只果蝇的概率；
（Ⅱ）求笼内至少剩下5只果蝇的概率.
（本小题满分１３分）
袋中有五张卡片，其中红色卡片三张，标号分别为1，2，3；蓝色卡片两张，标号分
为1，2.
(Ⅰ)从以上五张卡片中任取两张，求这两张卡片颜色不同且标号之和小于4的概率；
(Ⅱ)现袋中再放入一张标号为0的绿色卡片，从这六张卡片中任取两张，求这两张卡
片颜色不同且标号之和小于4的概率.