(右图为一简单集合体,其底面ABCD为正方形,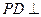 平面
平面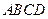 ,
,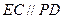 ,且
,且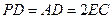 ="2" .
="2" .
(1)画出该几何体的三视图;
(2)求四棱锥B-CEPD的体积;
(3)求证: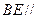 平面
平面 .
.
(本小题13分)已知数列{an}的前n项和Sn = 2an– 3×2n + 4 (n∈N*)
(1)求数列{an}的通项公式an;(2)设Tn为数列{Sn – 4}的前n项和,试比较Tn与14的大小.
(本小题满分13分)用一块长为a,宽为b (a>b)的矩形木块,在二面角为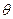 (0<
(0<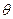 <
<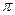 )的墙角处围出一个直三棱柱的储物仓(使木板垂直于地面,两边与墙面贴紧,另一边与地面贴紧),试问怎样围才能使储物仓的容积最大?并求出这个最大值.
)的墙角处围出一个直三棱柱的储物仓(使木板垂直于地面,两边与墙面贴紧,另一边与地面贴紧),试问怎样围才能使储物仓的容积最大?并求出这个最大值.
(本小题满分12分)一次智力竞赛中,共分三个环节:选答、抢答、风险选答,在第一环节“选答”中.每个选手可以从6道题(其中4道选择题,2道操作题)中任意选3道题作答,答对每道题可得100分;在第二环节“抢答”中,一共为参赛选手准备了5道抢答题.答对一道得1 00分,在每一道题的抢答中,每位选手抢到的概率是相等的;在第三环节“风险选答”中,一共为选手准备了A、B、C 三类不同的题目,选手每答对一道A类、B类、C类的题目将分别得到300分、200分、100分,但如果答错,则相应地要扣除300分、200分、100分.而选手答对一道A类、B类、C类题目的概率分别是0.6、0.7、0.8,现有甲、乙、丙三位选手参加比赛,试求:(1)乙选手在第一环节中,至少选中一道操作题的概率;
(2)甲选手在第二环节中抢到的题数多于乙选手而不多于丙选手的概率;(3)在第三环节中,就每道题而言,丙选手选择哪类题目得分的期望值更大.
(本小题满分12分)已知函数f (x) = a( ) + b.
) + b.
(1)当a = 1时,求f (x)的单调递减区间;(2)当a<0时,f (x)在[0,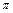 ]上的值域是[2,3],求a,b的值.
]上的值域是[2,3],求a,b的值.
本小题满分12分)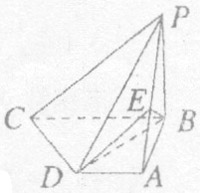
如图,在四棱锥P-ABCD中,PB⊥底面 ,CD⊥PD,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3,点E在棱PA上,且PE=2EA。(1)求异面直线PA与CD所成的角;(2)求证:PC∥平面EBD;(3)求二面角A-BE-D的大小。
,CD⊥PD,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3,点E在棱PA上,且PE=2EA。(1)求异面直线PA与CD所成的角;(2)求证:PC∥平面EBD;(3)求二面角A-BE-D的大小。