已知向量 ,
,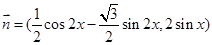 ,
,
设函数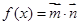 ,
, .
.
(Ⅰ)求函数 的最小正周期;
的最小正周期;
(Ⅱ)若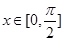 ,求函数
,求函数 值域.
值域.
某种产品按质量标准分成五个等级,等级编号 依次为1,2,3,4,5.现从一批产品中随机抽取20件,对其等级编号进行统计分析,得到频率分布表如下:
依次为1,2,3,4,5.现从一批产品中随机抽取20件,对其等级编号进行统计分析,得到频率分布表如下:
 |
1 |
2 |
3 |
4 |
5 |
| 频率 |
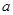 |
0.2 |
0.45 |
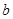 |
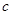 |
(I)若所抽取的20件产品中,等级编号为4的恰有3件,等级编号为5的恰有2件,求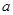 ,
,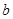 ,
,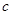 的值;
的值;
(Ⅱ)在(I)的条件下,将等级编号为4的3件产品记为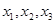 ,等级编号为5的2件产品记为
,等级编号为5的2件产品记为 ,现从
,现从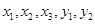 这5件产品中任取两件(假定每件产品被取出的可能性相同),写出所有可能的结果,并求这两件产品的等级编号恰好相同的概率.
这5件产品中任取两件(假定每件产品被取出的可能性相同),写出所有可能的结果,并求这两件产品的等级编号恰好相同的概率.
已知函数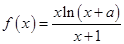
(Ⅰ)若函数 在
在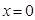 处取到极值,求
处取到极值,求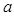 的值.
的值.
(Ⅱ)设定义在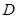 上的函数
上的函数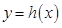 在点
在点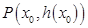 处的切线方程为
处的切线方程为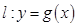 ,若
,若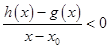 在
在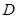 内恒成立,则称
内恒成立,则称 为函数的
为函数的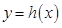 的“HOLD点”.当
的“HOLD点”.当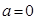 时,试问函数
时,试问函数 是否存在“HOLD点”,若存在,请至少求出一个“HOLD点”的横坐标;若不存在,请说明理由.
是否存在“HOLD点”,若存在,请至少求出一个“HOLD点”的横坐标;若不存在,请说明理由.
已知椭圆的中心在原点,焦点在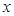 轴上,经过点
轴上,经过点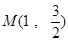 ,离心率
,离心率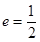 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)椭圆的左、右顶点分别为 、
、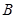 ,点
,点 为直线
为直线 上任意一点(点
上任意一点(点 不在
不在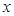 轴上),
轴上),
连结 交椭圆于
交椭圆于 点,连结
点,连结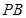 并延长交椭圆于
并延长交椭圆于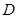 点,试问:是否存在
点,试问:是否存在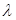 ,使得
,使得 成立,若存在,求出
成立,若存在,求出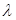 的值;若不存在,说明理由.
的值;若不存在,说明理由.
如图,已知平面
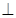 平面
平面 ,
, 与
与 分别是棱长为1与2的正三角形,
分别是棱长为1与2的正三角形, //
// ,四边形
,四边形 为直角梯形,
为直角梯形, //
// ,
, ,点
,点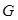 为
为 的重心,
的重心, 为
为 中点,
中点, ,
,
(Ⅰ)当 时,求证:
时,求证: //平面
//平面
(Ⅱ)若直线 与
与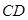 所成角为
所成角为 ,试求二面角
,试求二面角 的余弦值.
的余弦值.