(本小题满分9分)
如图5,一架飞机在空中P处探测到某高山山顶D处的俯角为60°,此后飞机以300米/秒的速度沿平行于地面AB的方向匀速飞行,飞行10秒到山顶D的正上方C处,此时测得飞机距地平面的垂直高度为12千米,求这座山的高(精确到0.1千米)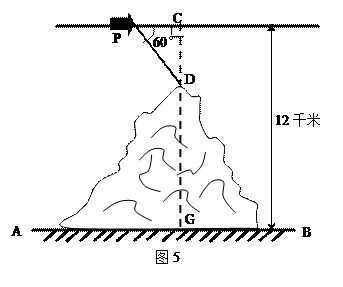
(1)解方程: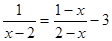 (2)解不等式组:
(2)解不等式组: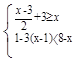 把解集在数轴上表示出来.
把解集在数轴上表示出来.
计算:
(1) (2
(2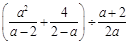
如图1,二次函数y=ax2+bx+c(a≠0)的图像与x轴交于点A、点B,与y轴交于点C,且A、B两点的坐标分别是(4,0)、(0,-2),tan∠BCO=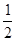 (1)求抛物线解析式;(2)点M为抛物线上一点,若以MB为直径的圆与直线BC相切于点B,求点M的坐标;(3) 如图2,若点P是抛物线上的动点,点Q是直线y=-x的动点,是否存在以点P、Q、C、O为顶点且以OC为一边的四边形是直角梯形;如果存在,请求出点P的坐标,如果不存在,请说明理由.
(1)求抛物线解析式;(2)点M为抛物线上一点,若以MB为直径的圆与直线BC相切于点B,求点M的坐标;(3) 如图2,若点P是抛物线上的动点,点Q是直线y=-x的动点,是否存在以点P、Q、C、O为顶点且以OC为一边的四边形是直角梯形;如果存在,请求出点P的坐标,如果不存在,请说明理由.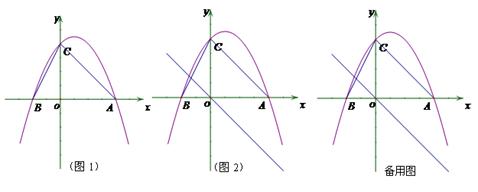
近年来,大学生就业日益困难.为了扶持大学生自主创业,某市政府提供了80万元无息贷款,用于某大学生开办公司生产并销售自主研发的一种电子产品,并约定用该公司经营的利润逐步偿还无息贷款.已知该产品的生产成本为每件40元,员工每人每月的工资为2500元,公司每月需支付其他费用15万元.该产品每月销售量y(万件)与销售单价x(元)之间的函数关系如图所示.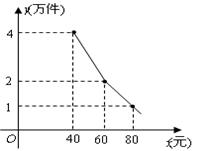
(1)分别求出40<x≤60;60<x<80时,月销售量y(万件)与销售
单价x(元)之间的函数关系;
(2)当销售单价定为50元时,为保证公司月利润达到5万元
(利润=销售额—生产成本—员工工资—其它费用),该公司
可安排员工多少人?
(3)若该公司有80名员工,则该公司最早可在几月后还清贷款?
如图1,点A在反比例函数y= 的图象上,AC⊥x轴,垂足为C,且△AOC的面积为
的图象上,AC⊥x轴,垂足为C,且△AOC的面积为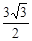 .(1)求反比例函数的解析式;
.(1)求反比例函数的解析式;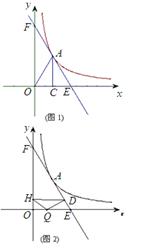
(2)当点A的横坐标为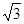 ,过点A的直线交x、y轴于E、F两点,且△EOF以点A为外心,求这条直线的解析式;
,过点A的直线交x、y轴于E、F两点,且△EOF以点A为外心,求这条直线的解析式;
(3)如图2,在(2)下,若Q是OE上不与O、E重合的任意一点,QD⊥EF于D,DH⊥y轴于H,在线段OE上是否存在点Q,使QH∥EF?若存在这样的点,请求出点Q的坐标;若不存在,请说明理由.