近年来，大学生就业日益困难．为了扶持大学生自主创业，某市政府提供了80万元无息贷款，用于某大学生开办公司生产并销售自主研发的一种电子产品，并约定用该公司经营的利润逐步偿还无息贷款．已知该产品的生产成本为每件40元，员工每人每月的工资为2500元，公司每月需支付其他费用15万元．该产品每月销售量y(万件)与销售单价x(元)之间的函数关系如图所示．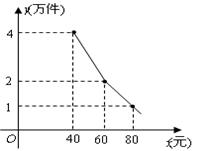
(1)分别求出40＜x≤60；60＜x＜80时，月销售量y(万件)与销售
单价x(元)之间的函数关系；
(2)当销售单价定为50元时，为保证公司月利润达到5万元
(利润＝销售额—生产成本—员工工资—其它费用)，该公司
可安排员工多少人？
(3)若该公司有80名员工，则该公司最早可在几月后还清贷款？
(
)经过
、
两点，抛物线与
轴交点为
，其顶点为
，连接
，点
是线段
、
，连接
。
)，
的面积为
，求
的函数关系式，写出自变量
，连接
，把
沿直线
，请直接写出