(本小题满分14分)
现有甲,乙,丙,丁四名篮球运动员进行传球训练,由甲开始传球(即第一次传球是由甲传向乙或丙或丁),记第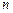 次传球球传回到甲的不同传球方式种数为
次传球球传回到甲的不同传球方式种数为 .
.
(1)试写出 ,
, 并找出
并找出 与
与 (
( )的关系式;
)的关系式;
(2)求数列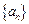 的通项公式;
的通项公式;
(3)证明:当 时,
时, 
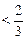 .
.
(本小题满分12分)
为备战2012奥运会,甲、乙两位射击选手进行了强化训练. 现分别从他们的强化训练期间的若干次平均成绩中随机抽取8次,记录如下:
甲:8.3,9.0,7.9,7.8,9.4,8.9,8.4,8.3;
乙:9.2,9.5,8.0,7.5,8.2,8.1,9.0,8.5.
(1)画出甲、乙两位选手成绩的茎叶图;(用茎表示成绩的整数部分,用叶表示成绩的小数部分)
(2)现要从中选派一人参加奥运会,从平均成绩和发挥稳定性角度考虑,你认为派哪位选手参加合理? 简单说明理由.
(3)若将频率视为概率,对选手乙在今后的三次比赛成绩进行预测,记这三次成绩中不低于8.5分的次数为 ,求
,求 的分布列及均值E
的分布列及均值E .
.
(本小题满分12分)
已知点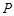 是圆
是圆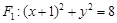 上任意一点,点
上任意一点,点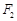 与点
与点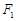 关于原点对称.线段
关于原点对称.线段 的中垂线
的中垂线 分别与
分别与 交于
交于 两点.
两点.
(1)求点 的轨迹
的轨迹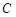 的方程;
的方程;
(2)斜率为1的直线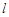 与曲线
与曲线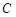 交于
交于 两点,若
两点,若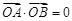 (
( 为坐标原点),求直线
为坐标原点),求直线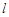 的方程.
的方程.
(本小题满分12分)
如图,在四棱锥S—ABCD中,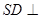 底面ABCD,底面ABCD是矩形,
底面ABCD,底面ABCD是矩形,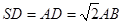 ,E是SA的中点.
,E是SA的中点.
(1)求证:平面BED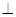 平面SAB;
平面SAB;
(2)求直线SA与平面BED所成角的大小.
(本小题满分14分)已知函数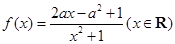 ,其中
,其中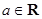 .
.
(Ⅰ)当 时,求曲线
时,求曲线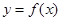 在点
在点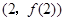 处的切线方程;
处的切线方程;
(Ⅱ)当 时,求函数
时,求函数 的单调区间与极值.
的单调区间与极值.
(本小题满分14分)已知圆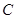 过点
过点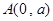
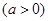 , 且在
, 且在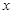 轴上截得的弦
轴上截得的弦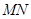 的长为
的长为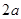 .
.
(1) 求圆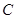 的圆心的轨迹方程;
的圆心的轨迹方程;
(2) 若 , 求圆
, 求圆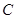 的方程.
的方程.