设数列{an}满足an+1=2an+n2-4n+1.
(1)若a1=3,求证:存在 (a,b,c为常数),使数列{an+f(n)}是等比数列,并求出数列{an}的通项公式;
(a,b,c为常数),使数列{an+f(n)}是等比数列,并求出数列{an}的通项公式;
(2)若an是一个等差数列{bn}的前n项和,求首项a1的值与数列{bn}的通项公式.
已知函数
 的图象的两相邻对称轴间的距离为
的图象的两相邻对称轴间的距离为 .
.
(1)求值;
(2)若 ,且有且仅有一个实根,求实数
,且有且仅有一个实根,求实数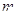 的值.
的值.
设命题 :函数
:函数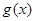 =
= 是
是 上的减函数,命题
上的减函数,命题 :函数
:函数 的定义域为
的定义域为 ,若“
,若“ 且
且 ”为假命题,“
”为假命题,“ 或
或 ”为真命题,求实数
”为真命题,求实数 的取值范围.
的取值范围.
(本小题满分14分)
已知函数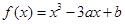 在
在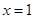 处有极小值
处有极小值 。
。
(1)求函数 的解析式;
的解析式;
(2)若函数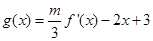 在
在 只有一个零点,求
只有一个零点,求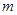 的取值范围。
的取值范围。
(本小题满分14分)
已知,圆C: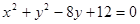 ,直线
,直线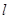 :
: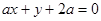 .
.
(1) 当a为何值时,直线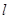 与圆C相切;
与圆C相切;
(2) 当直线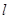 与圆C相交于A、B两点,且
与圆C相交于A、B两点,且 时,求直线
时,求直线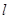 的方程.
的方程.
(本小题满分14分)
已知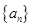 是首项为19,公差为-4的等差数列,
是首项为19,公差为-4的等差数列,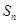 为
为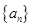 的前
的前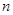 项和.
项和.
(Ⅰ)求通项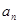 及
及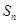 ;
;
(Ⅱ)设 是首项为1,公比为2的等比数列,求数列
是首项为1,公比为2的等比数列,求数列 的通项公式及其前
的通项公式及其前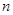 项和
项和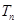 .
.