(本小题满分12分)
已知定点A(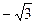
,0),B是圆C:(x-
)2+y2=16,(C为圆心)上的动点,AB的垂直平分线与BC交与点E.
(1)求动点E的轨迹方程.
(2)设直线l:y="kx+m" (k≠0,m>0)与E的轨迹交与P,Q两点,且以PQ为对角线的菱形的一顶点为M(-1,0),求△OPQ面积的最大值及此时直线l的方程.
计算下列定积分。
（1）
（2） 
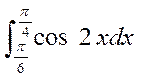（3）
一机器可以按各种不同速度运转，其生产的产品有一些会有缺点，每小时生产有缺点的产品数随机器运转速度的不同而变化。下表为其试验数据：
| 速度（x转/秒） |
每小时生产有缺点的产品数（y个） |
||
| 8 |
6 |
||
| 9 |
8 |
||
| 10 |
10 |
||
| 13 |
12 |
（1）、画出散点图；
（2）、求机器运转速度与每小时生产有缺点的产品数之间的回归方程；（系数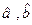
用分数表示）
（3）、若实际生产所允许的每小时生产有缺点的产品数不超过10件，那么机器的速度每秒不超过多少转？
某高中课外活动小组调查了100名男生与100名女生报考文、理科的情况，下图为其等高条形图：
（1）绘出2×2列联表；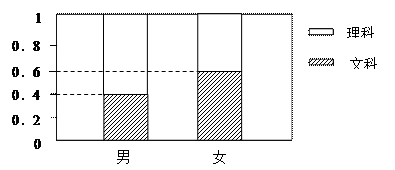
（2）利用独
立性检验方法判断性别与报考文、理科是否有关系？若有关系，所得结论的把握
有多大？
通过计算可得下列等式：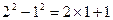
┅┅
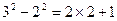
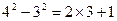
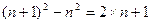
将以上各式分别相加得：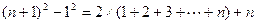
即：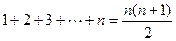
类比上述求法：请你求出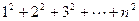
的值.
若下列方程：
，
，
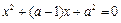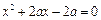，至少有一个方程有实根，试求实数
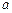的取值范围．
