有甲乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表.
| |
优秀 |
非优秀 |
总计 |
| 甲班 |
10 |
|
|
| 乙班 |
|
30 |
|
| 合计 |
|
|
105 |
已知在全部105人中抽到随机抽取1人为优秀的概率为
(1)请完成上面的列联表;
(2)根据列联表的数据,若按 的可靠性要求,能否认为“成绩与班级有关系” .
的可靠性要求,能否认为“成绩与班级有关系” .
(3)若按下面的方法从甲班优秀的学生抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到6或10号的概率.
解下列不等式:
(1)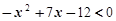 ;(2)
;(2)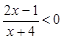 .
.
已知函数 满足
满足 , 且对于任意
, 且对于任意 恒有
恒有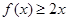 成立。
成立。
(1) 求实数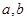 的值;
的值;
(2)设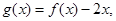 若存在实数
若存在实数 ,当
,当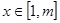 时,
时,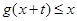 恒成立,求实数
恒成立,求实数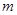 的最大值。
的最大值。
我市某蔬菜种植户计划建造一个室内面积为800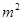 的矩形蔬菜温室,在温室内,沿左、右两侧与后侧内墙各保留1
的矩形蔬菜温室,在温室内,沿左、右两侧与后侧内墙各保留1 宽的通道,沿前侧内墙保留3
宽的通道,沿前侧内墙保留3 宽的空地(如图),中间部分种植蔬菜。
宽的空地(如图),中间部分种植蔬菜。
(1)当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积是多少?
(2)由于受地形条件的限制,矩形温室的边长不得少于25 ,则蔬菜的最大种植面积是多少?
,则蔬菜的最大种植面积是多少?
已知不等式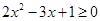 的解集为
的解集为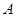 ,不等式
,不等式 的解集为
的解集为 ,
,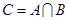 .
.
(1)求集合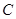 ;
;
(2)若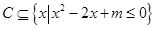 ,求实数
,求实数 的取值范围;
的取值范围;
(3)若存在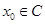 ,使得不等式
,使得不等式 成立, 求实数
成立, 求实数 的取值范围.
的取值范围.
已知命题p:函数y=xm在(0,+∞)为减函数命题q:复数z=m2-5m-6+(m-2)i,(m∈R)在复平面内的对应点在第三象限.如果p或q为真命题,p且q为假命题,求m的取值范围.