(本小题满分12分)
设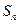 为数列{
为数列{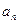 }的前n项和,
}的前n项和,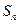 =kn2+n,n∈N*,其中k是常数.
=kn2+n,n∈N*,其中k是常数.
(1)求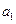 及
及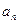 ;
;
(2)若对于任意的m∈N*, ,
, ,
, 成等比数列,求k的值.
成等比数列,求k的值.
某营养师要为某个儿童预订午餐和晚餐.已知一个单位的午餐含12个单位的碳水化合物、6个单位的蛋白质和6个单位的维生素C;一个单位的晚餐含8个单位的碳水化合物、6个单位的蛋白质和10个单位的维生素C.另外,该儿童这两餐需要的营养中至少含64个单位的碳水化合物、42个单位的蛋白质和54个单位的维生素C.
如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?
已知x,y满足约束条件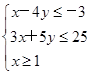 ,试求解下列问题.
,试求解下列问题.
(1)z= 的最大值和最小值;
的最大值和最小值;
(2)z=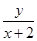 的最大值和最小值;
的最大值和最小值;
(3)z=|3x+4y+3|的最大值和最小值.
设z=2y-2x+4,其中x、y满足条件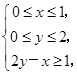 求z的最大值和最小值.
求z的最大值和最小值.
某公司计划2013年在甲、乙两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元,甲、乙电视台的广告收费标准分别为500元/分钟和200元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告能给公司带来的收益分别为0.3万元和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
某公司生产甲、乙两种桶装产品.已知生产甲产品1桶需耗A原料1kg、B原料2kg;生产乙产品1桶需耗A原料2kg,B原料1kg.每桶甲产品的利润是300元,每桶乙产品的利润是400元.公司在生产这两种产品的计划中,要求每天消耗A、B原料都不超过12kg.通过合理安排生产计划,从每天生产的甲、乙两种产品中,公司共可获得的最大利润是多少?