某公司计划2013年在甲、乙两个电视台做总时间不超过300分钟的广告，广告总费用不超过9万元，甲、乙电视台的广告收费标准分别为500元/分钟和200元/分钟，规定甲、乙两个电视台为该公司所做的每分钟广告能给公司带来的收益分别为0.3万元和0.2万元．问该公司如何分配在甲、乙两个电视台的广告时间，才能使公司的收益最大，最大收益是多少万元？
.4.命题
方程
有两个不等的正实数根，命题
方程
无实数根。若“
或
”为真命题，求
的取值范围。
(本小题满分14分)
设函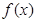数
对任意实数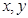
都有
且
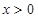时
。
(Ⅰ)证明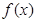是奇函数；
(Ⅱ)证明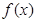在
内是增函数；
(Ⅲ)若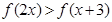
，试求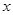
的取值范围。
（本小题满分14分）如图，
在正方体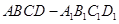
中，棱长是1，
（1）求证：
；
（2）求点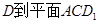
的距离。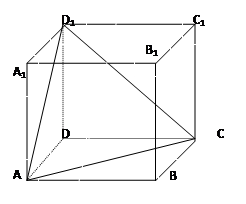
（本小题满分14分）
已知直线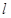
的方程是
，点
。
(1) 求过点
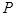且与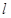平行的直线方程
（2）求过点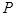且与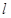垂直的直线方程
（1）等比数列
中，对任意
，
时都有
成等差，求公比
的值
（2）设
是等比数列的前
项和，当
成等差时，是否有
一定也成等差数列？说明理由
（3）设等比数列的公比为，前项和为，是否存在正整数
，使
成等差且
也成等差，若存在，求出与满足的关系；若不存在，请说明理由