(1)等比数列 中,对任意
中,对任意 ,
, 时都有
时都有 成等差,求公比
成等差,求公比 的值
的值
(2)设 是等比数列
是等比数列 的前
的前 项和,当
项和,当 成等差时,是否有
成等差时,是否有 一定也成等差数列?说明理由
一定也成等差数列?说明理由
(3)设等比数列 的公比为
的公比为 ,前
,前 项和为
项和为 ,是否存在正整数
,是否存在正整数 ,使
,使 成等差且
成等差且 也成等差,若存在,求出
也成等差,若存在,求出 与
与 满足的关系;若不存在,请说明理由
满足的关系;若不存在,请说明理由
成等差数列的三个正数的和等于15,并且这三个数分别加上2,5,13后成为等比数列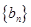 中的
中的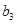 ,
,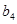 ,
,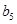 .
.
(I) 求数列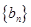 的通项公式;
的通项公式;
(II) 数列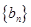 的前n项和为
的前n项和为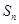 ,求证:数列
,求证:数列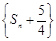 是等比数列.
是等比数列.
已知函数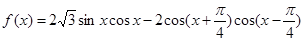 .
.
(I)求函数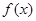 的最小正周期和图象的对称轴方程;
的最小正周期和图象的对称轴方程;
(II)求函数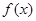 在区间
在区间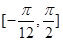 上的值域.
上的值域.
(本小题满分12分)
已知函数f(x)=-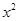 +x+lnx,g(x)=
+x+lnx,g(x)=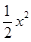 +
+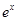 -x
-x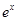 .
.
(Ⅰ)判断函数f(x)的零点的个数,并说明理由;
(Ⅱ)当x∈[-2,2]时,函数g(x)的图像总在直线y=a-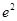 的上方,求实数a的取值范围.
的上方,求实数a的取值范围.
(本小题满分12分)
某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据
| x |
6 |
8 |
10 |
12 |
| y |
2 |
3 |
5 |
6 |
(Ⅰ)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程y=bx+a;
(Ⅱ)试根据(Ⅰ)求出的线性回归方程,预测记忆力为9的同学的判断力.
(相关公式:b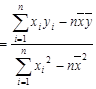 ,a
,a )
)
(本小题满分12分)
椭圆C的中心在坐标原点,焦点在x轴上,右焦点F的坐标为(2,0),且点F到短轴的一个端点的距离是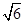 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点F作斜率为k的直线l,与椭圆C交于A、B两点,若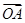 ·
·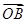 >-
>-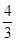 ,求k的取值范围.
,求k的取值范围.