(本小题满分13分)
在数列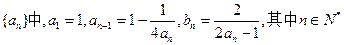 。
。
(1)求证:数列 是等差数列,并求数列
是等差数列,并求数列 的通项公式
的通项公式 ;
;
(2)设 ,求数列
,求数列 的前
的前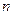 项和。
项和。
(本小题 满分12分)
满分12分)
已知曲线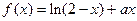 在点
在点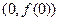 处的切
处的切 线斜率为
线斜率为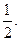
(Ⅰ)求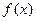 的极值;
的极值;
(Ⅱ)设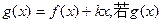 在(一∞,1)上是增函数,求实数
在(一∞,1)上是增函数,求实数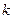 的取值范围;
的取值范围;
已知四棱锥P—ABCD中,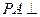 平面ABCD,底面ABCD为菱形,
平面ABCD,底面ABCD为菱形,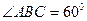 ,AB=PA=2,E.F分别为BC.PD的中点。
,AB=PA=2,E.F分别为BC.PD的中点。
(Ⅰ)求证:PB//平面AFC;
(Ⅱ)求平面PAE与平面PCD所成锐二面角的余弦值。
国庆前夕,我国具有自主知识产权的“人甲型H1N1流感病毒核酸检测试剂盒”(简称试剂盒)在上海进行批量生产,这种“试剂盒”不仅成本低操作简单,而且可以准确诊断出“甲流感”病情,为甲型H1N1流感疫情的防控再添一道安全屏障.某医院在得到 “试剂盒”的第一时间,特别选择了知道诊断结论的5位发热病人(其中“甲流感”患者只占少数),对病情做
“试剂盒”的第一时间,特别选择了知道诊断结论的5位发热病人(其中“甲流感”患者只占少数),对病情做 了一次验证性检测.已知如果任意抽检2人,恰有1位是“甲流感”患者的概率为
了一次验证性检测.已知如果任意抽检2人,恰有1位是“甲流感”患者的概率为 。
。
(1)求出这5位发热病人中“甲流感”患者 的人数
的人数 ;
;
(2)若用“试剂盒”逐个检测这5位发热病人,直到能确定“甲流感”患者为止,设ξ表示检测次数,求ξ的分布列及数学期望Eξ。
设函数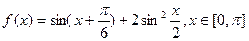
(Ⅰ)求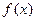 的值域;
的值域;
(Ⅱ)记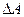 BC的内角A.B.C的对边长分别为
BC的内角A.B.C的对边长分别为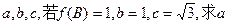 的值。
的值。
已知函数 是
是 ,的一个极值点
,的一个极值点
(I)求a的值;
(II)证明: •
•