某公司生产甲、乙两种桶装产品.已知生产甲产品1桶需耗A原料1kg、B原料2kg;生产乙产品1桶需耗A原料2kg,B原料1kg.每桶甲产品的利润是300元,每桶乙产品的利润是400元.公司在生产这两种产品的计划中,要求每天消耗A、B原料都不超过12kg.通过合理安排生产计划,从每天生产的甲、乙两种产品中,公司共可获得的最大利润是多少?
已知焦点在X轴上的椭圆C为. ,F1、F2分别是椭圆C的左、右焦点,离心率e=
,F1、F2分别是椭圆C的左、右焦点,离心率e=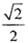 .
.
(I )求椭圆C的方程;
(II) 设点Q的坐标为(1,0),椭圆上是否存在一点P,使得直线 都与以Q为圆心的一个圆相切,如存在,求出P点坐标及圆的方程,如不存在,请说明理由.
都与以Q为圆心的一个圆相切,如存在,求出P点坐标及圆的方程,如不存在,请说明理由.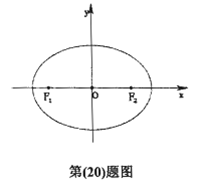
若数列 满足:
满足:
(I) 证明数列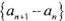 是等差数列;.
是等差数列;.
(II) 求使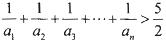 成立的最小的正整数n
成立的最小的正整数n
如图1所示,在边长为12的正方形 中,点B、C在线段AD上,且AB = 3,BC = 4,作
中,点B、C在线段AD上,且AB = 3,BC = 4,作 分别交
分别交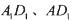 于点B,P,作
于点B,P,作 分别交
分别交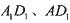 于点
于点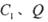 ,将该正方形沿
,将该正方形沿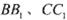 折叠,使得
折叠,使得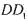 与
与 重合,构成如图2所示的三棱柱
重合,构成如图2所示的三棱柱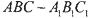
(I )求证: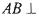 平面
平面 ;
;
(II)求多面体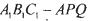 的体积.
的体积.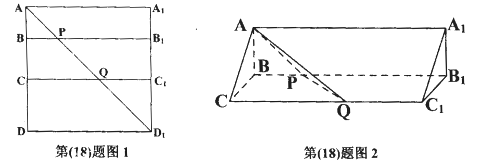
2011.年广州亚运会的一组志愿者全部通晓中文,并且每个志愿者还都通晓英语、日语和韩语中的一种(但无人通晓两种外语).已知从中任抽一人,其通晓中文和英语的概率为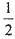 ,通晓中文和日语的概率为
,通晓中文和日语的概率为 .若通晓中文和韩语的人数不超过3人.
.若通晓中文和韩语的人数不超过3人.
(I )求这组志愿者的人数;
(II)现从这组志愿者中选出通晓英语的志愿者1名,通晓韩语的志愿者1名,若甲通晓英语,乙通晓韩语,求甲和乙不全被选中的概率.
己知函数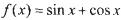 .
.
(I )若,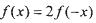 ,求
,求 的值;
的值;
(II)求函数 的最大值和单调递增区间.
的最大值和单调递增区间.