(满分14分)如图,⊙O的半径为1,点P是⊙O上一点,弦AB垂直平分线段OP,点D是劣弧AB上任一点(与端点A、B不重合),DE⊥AB于点E,以点D为圆心、DE长为半径作⊙D,分别过点A、B作⊙D的切线,两条切线相交于点C.
(1)求弦AB的长;
(2)判断∠ACB是否为定值,若是,求出∠ACB的大小;否则,请说明理由;
(3)记△ABC的面积为S,若 ,求△ABC的周长.
,求△ABC的周长.
(本题满分8分,每题4分)
(1)解方程: x2-4x-3=0(2)解不等式组: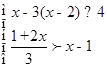
(本题满分8分,每题4分)计算:
(1)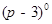 +2sin45°-
+2sin45°-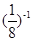
(2)2(a+1)-(3-a)(3+a)-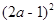
(本题12分) 如图,已知直线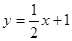 与
与 轴交于点
轴交于点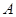 ,与
,与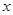 轴交于点
轴交于点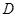 ,抛物线
,抛物线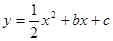 与直线交于
与直线交于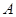 、
、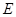 两点,与
两点,与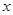 轴交于
轴交于 、
、 两点,且
两点,且 点坐标为(1,0).
点坐标为(1,0).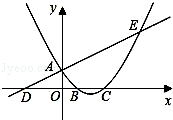
(1)求该抛物线的解析式;
(2)动点 在
在 轴上移动,当△
轴上移动,当△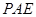 是直角三角形时,直接写出点
是直角三角形时,直接写出点 的坐标;
的坐标;
(3)在抛物线的对称轴上找一点 ,使|
,使|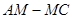 |的值最大,求出点
|的值最大,求出点 的坐标.
的坐标.
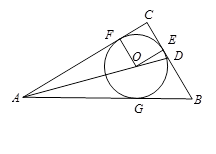
(本题10分)如图,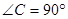 ,⊙
,⊙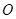 是Rt△
是Rt△ 的内切圆,分别切
的内切圆,分别切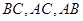 于点
于点 ,连接
,连接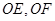 .
.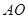 的延长线交
的延长线交 于点
于点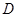 ,
,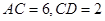 .
.
(1)求证:四边形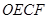 为正方形;
为正方形;
(2)求⊙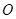 的半径; (3)求
的半径; (3)求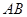 的长.
的长.
(本题8分)某乡镇决定对A、B两村之间的公路进行改造,并有甲工程队从A村向B村方向修筑,乙工程队从B村向A村方向修筑.已知甲工程队先施工3天,乙工程队再开始施工.乙工程队施工几天后因另有任务提前离开,余下的任务有甲工程队单独完成,直到公路修通.下图是甲乙两个工程队修公路的长度y(米)与施工时间x(天)之间的函数图象,请根据图象所提供的信息解答下列问题:
(1)乙工程队每天修公路多少米?
(2)分别求甲、乙工程队修公路的长度y(米)与施工时间x(天)之间的函数关系式.
(3)若该项工程由甲、乙两工程队一直合作施工,需几天完成?