已知函数,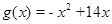 .
.
(1)求函数 在点
在点 处的切线方程;
处的切线方程;
(2)若函数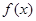 与
与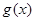 在区间
在区间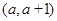 上均为增函数,求
上均为增函数,求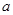 的取值范围;
的取值范围;
(3)若方程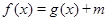 有唯一解,试求实数
有唯一解,试求实数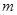 的值.
的值.
设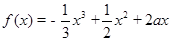
(1)若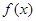 在
在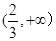 上存在单调递增区间,求
上存在单调递增区间,求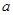 的取值范围;
的取值范围;
(2)当a=1时,求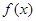 在
在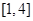 上的最值.
上的最值.
已知函数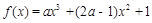 ,当
,当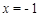 时,函数
时,函数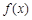 取得极值.
取得极值.
(1)求实数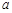 的值;
的值;
(2)确定函数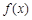 的单调区间
的单调区间
甲乙两人约定在下午六点到七点之间在某处会面,并约定先到者应等候另一人20分钟,过时即可离去,求两人能会面的概率。
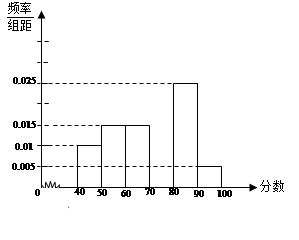
某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60) ...[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)求成绩落在[70,80)上的频率,并补全这个频率分布直方图;
(Ⅱ) 估计这次考试的及格率(60分及以上为及格)和平均分;
(Ⅲ) 从成绩是70分以上(包括70分)的学生中选两人,求他们在同一分数段的概率.