已知函数f(x)=x3-ax2-3x.
(1)若f(x)在区间[1,+∞)上是增函数,求实数a的取值范围;
(2)若x=- 是f(x)的极值点,求
是f(x)的极值点,求 f(x)在[1,a]上的最大值;
f(x)在[1,a]上的最大值;
(3)在(2)的条件下,是否存在实数b,使得函数g(x)=bx的图象与函数f(x)的图象恰有3个交点,若存在,请求出实数b的取值范围;若不存在,试说明理由.
.本小题满分14分)
已知定义在实数集R上的偶函数 的最小值为3,且当
的最小值为3,且当 时,
时,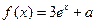 ,其中e是自然对数的底数
,其中e是自然对数的底数 。
。
(1)求函数 的解析式;
的解析式;
(2)若实数 使得存在
使得存在 ,只要
,只要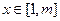 ,就有
,就有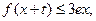 求正整
求正整
数n的最大值。
.已知定圆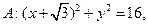 圆心为A;动圆M过点
圆心为A;动圆M过点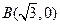 且与圆A相切,圆心M 的坐标为
且与圆A相切,圆心M 的坐标为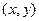 且
且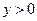 ,它的轨迹记为
,它的轨迹记为 C。
C。
(1)求曲线 C的方程;
C的方程;
(2)过一点N(1,0)作两条互相垂直的直线与曲线C分别交于点P和Q,试问这两条直线能否使得向量 互相垂直?若存在,求出点P,Q的横坐标,若不存在,请说明理由。
互相垂直?若存在,求出点P,Q的横坐标,若不存在,请说明理由。
.(本小题满分12分)
如图所示,有公共边的两正方形ABB1A1与BCC1B1的边AB、BC均在平面α内,且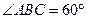 ,M是BC的中点,点N在C1C上。
,M是BC的中点,点N在C1C上。
(1)试确定点 N的位置,使
N的位置,使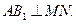
(2)当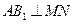 时,求二面角M—AB1—N的余弦值。
时,求二面角M—AB1—N的余弦值。
.(本小题满分12分)
鲜花扫墓渐流行,清明节期间,吉安某鲜花店某种鲜花的进货价为每束10元,销售价为每束20元,若在清明节期间内没有售 完,则在清明节营业结束后以每束5元的价格处理,据前5年的有关资料统计,这种
完,则在清明节营业结束后以每束5元的价格处理,据前5年的有关资料统计,这种 鲜花的需
鲜花的需 求量X(束)服从以下分布:
求量X(束)服从以下分布:
| X |
20 |
30 |
40 |
50 |
| P |
0.20 |
0. 35 35 |
a |
0.15 |
(1)求a的值;
(2)当进货量为20,30束时,分别求出该店获利润的期望值;
(3)该店今年清明节前进该种鲜花多少束为宜?
.(本小题满分12分)
已知函数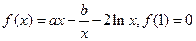 ,若函数
,若函数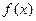 的图象在x=1处的切线平行于x轴且数列
的图象在x=1处的切线平行于x轴且数列 满足
满足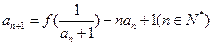
(1)求当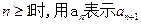 的关系式;
的关系式;
(2)若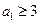 ,求证:任意
,求证:任意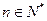 ,都有
,都有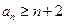 成立。
成立。