(本大题满分12分)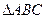 中角A的对边长等于2,向量
中角A的对边长等于2,向量 向量
向量 .
.
(1)当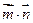 取最大值时,求角A的大小;
取最大值时,求角A的大小;
(2)在(1)条件下,求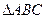 面积的最大值.
面积的最大值.
(满分13分)如图所示,将一个圆形的画板分成面积相等的三部分,
每部分上分别涂色为黄、红、蓝三色,某人随机向画板投射一只镖,
如果射中边界则重新再射,射中涂色部分则分别得分为3,2, 1分,
投射两次的得分为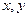 ,记
,记 .
.
求随机变量 的最大值,并求事件“
的最大值,并求事件“ 取得最大值”的概率.
取得最大值”的概率.
 |
(满分13分)某项实验,在100次实验中成功率只有10%,进行技术改造后,又进行了100次实验,若要有97.5%以上的把握认为“技术改造效果明显”,实验的成功率最小应是多少?(设 ,
,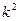 的观测值为
的观测值为 )
)
(解答过程须列出列联表)

(本小题满分14分)
在平面直角坐标系 中,已知圆
中,已知圆 和圆
和圆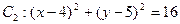 .
.
(1)若直线 过点
过点 ,且被圆
,且被圆
 截得的弦长为
截得的弦长为 ,求直线
,求直线 的方程;
的方程;
(2)在平面内是否存在一点 ,使得过点
,使得过点 有无穷多对互相垂直的直线
有无穷多对互相垂直的直线 和
和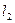 ,它们分别与圆
,它们分别与圆 和圆
和圆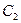 相交,且直线
相交,且直线 被圆
被圆 截得的弦长的
截得的弦长的 倍与直线
倍与直线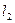 被圆
被圆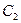 截得的弦长相等?若存在,求出所有满足条件的
截得的弦长相等?若存在,求出所有满足条件的 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
 |
(本小题满分14分)
如图,已知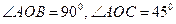 ,
,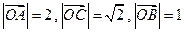 .
.
(1)试用向量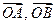 来表示向量
来表示向量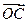 ;
;
(2)若向量 ,
,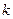
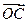 的终点在一条直线上,
的终点在一条直线上,
求实数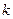 的值;
的值;
(3 )设
)设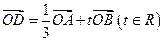 ,当
,当 、
、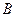 、
、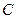 、
、 四点共圆时, 求
四点共圆时, 求 的值.
的值.
 |