（本小题满分12分）
函数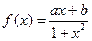
是定义域在（－1，1）上的奇函数，且
.
（1）确定函数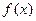
的解析式；
（2）用定义证明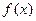在（－1，1）上是增函数；
（3）解不等式
.
如图，
是的内接三角形，PA是圆O的切线，切点为A，PB交AC于点E，交圆O于点D，PA=PE，
，PD=1，DB=8.
（1）求
的面积；
（2）求弦AC的长.
已知函数
.
（1）当
时，证明：当
时，
；
（2）当
时，证明：
.
如图
为椭圆C：
的左、右焦点，D，E是椭圆的两个顶点，椭圆的离心率
，
的面积为
.若点
在椭圆C上，则点
称为点M的一个“椭圆”，直线
与椭圆交于A，B两点，A，B两点的“椭圆”分别为P，Q.
（1）求椭圆C的标准方程；
（2）问是否存在过左焦点
的直线，使得以PQ为直径的圆经过坐标原点？若存在，求出该直线的方程；若不存在，请说明理由.
如图，在四棱柱
中，底面ABCD和侧面
都是矩形，E是CD的中点，
，
.
（1）求证：
；
（2）若平面与平面
所成的锐二面角的大小为
，求线段
的长度.
由某种设备的使用年限
（年）与所支出的维修费
（万元）的数据资料算得如下结果，
，
，
，
.
（1）求所支出的维修费y对使用年限x的线性回归方程
；
（2）①判断变量x与y之间是正相关还是负相关；
②当使用年限为8年时，试估计支出的维修费是多少.
（附：在线性回归方程中，）
，
，其中
，
为样本平均值.)