(8分)
(1)计算:
(2)解方程:
(本小题满分12分)已知:抛物线 的对称轴为
的对称轴为 与
与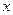 轴交于
轴交于 两点,与
两点,与 轴交于点
轴交于点 其中
其中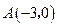 、
、

(1)求这条抛物线的函数表达式.
(2)已知在对称轴上存在一点P,使得 的周长最小.请求出点P的坐标.
的周长最小.请求出点P的坐标.
(3)若点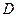 是线段
是线段 上的一个动点(不与点O、点C重合).过点D作
上的一个动点(不与点O、点C重合).过点D作 交
交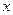 轴于点
轴于点 连接
连接 、
、 .设
.设 的长为
的长为 ,
, 的面积为
的面积为 .求
.求 与
与 之间的函数关系式.试说明
之间的函数关系式.试说明 是否存在最大值,若存在,请求出最大值;若不存在,请说明理由.
是否存在最大值,若存在,请求出最大值;若不存在,请说明理由.
(本小题满分12分)如图, 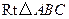 内接于
内接于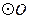 ,
,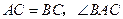 的平分线
的平分线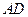 与
与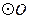 交于点
交于点 ,与
,与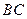 交于点
交于点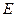 ,延长
,延长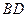 ,与
,与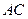 的延长线交于点
的延长线交于点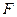 ,连接
,连接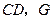 是
是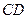 的中点,连结
的中点,连结 .
.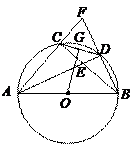
(1)判断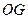 与
与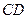 的位置关系,写出你的结论并证明;
的位置关系,写出你的结论并证明;
(2)求证: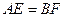 ;
;
(3)若 ,求
,求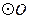 的面积.
的面积.
(本小题满分10分)有3个完全相同的小球,把它们分别标号为1,2,3,放在一个口袋中,随机地摸出一个小球不放回,再随机地摸出一个小球.
(Ⅰ)采用树形图法(或列表法)列出两次摸球出现的所有可能结果;
(Ⅱ)求摸出的两个球号码之和等于5的概率.
(本小题满分10分)已知图中的曲线是反比例函数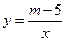 (
(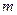 为常数)图象的一支.
为常数)图象的一支.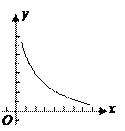
(Ⅰ)这个反比例函数图象的另一支在第几象限?常数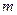 的取值范围是什么?
的取值范围是什么?
(Ⅱ)若该函数的图象与正比例函数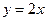 的图象在第一象内限的交点为
的图象在第一象内限的交点为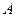 ,过
,过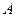 点作
点作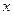 轴的垂线,垂足为
轴的垂线,垂足为 ,当
,当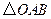 的面积为4时,求点
的面积为4时,求点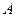 的坐标及反比例函数的解析式.
的坐标及反比例函数的解析式.
(本小题满分8分)市种子培育基地用 、
、 、
、 三种型号的甜玉米种子共1500粒进行发芽试验,从中选出发芽率高的种子进行推广,通过试验知道,
三种型号的甜玉米种子共1500粒进行发芽试验,从中选出发芽率高的种子进行推广,通过试验知道, 型号种子的发芽率为
型号种子的发芽率为 .根据试验数据绘制了下面两个不完整的统计图(图1、图2):
.根据试验数据绘制了下面两个不完整的统计图(图1、图2):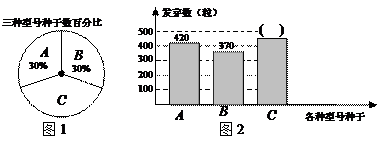
(1) 型号种子的发芽数是_________粒;
型号种子的发芽数是_________粒;
(2)通过计算说明,应选哪种型号的种子进行推广?(精确到 )
)
(3)如果将所有已发芽的种子放到一起,从中随机取出一粒,求取到 型号发芽种子的概率.
型号发芽种子的概率.