(本小题满分 分)
分)
在股票市场上,投资者常参考 股价(每一股的价格)的某条平滑均线(记作 )的变化情况来决定买入或卖出股票.股民老张在研究股票的走势图时,发现一只股票的
)的变化情况来决定买入或卖出股票.股民老张在研究股票的走势图时,发现一只股票的 均线近期走得很有特点:如果按如图所示的方式建立平面直角坐标系
均线近期走得很有特点:如果按如图所示的方式建立平面直角坐标系 ,则股价
,则股价 (元)和时间
(元)和时间 的关系在
的关系在 段可近似地用解析式
段可近似地用解析式 (
( )来描述,从
)来描述,从 点走到今天的
点走到今天的 点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且
点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且 点和
点和 点正好关于直线
点正好关于直线 对称.老张预计这只股票未来的走势如图中虚线所示,这里
对称.老张预计这只股票未来的走势如图中虚线所示,这里 段与
段与 段关于直线
段关于直线 对称,
对称, 段是股价延续
段是股价延续 段的趋势(规律)走到这波上升行情的最高点
段的趋势(规律)走到这波上升行情的最高点 .
.
现在老张决定取点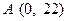 ,点
,点 ,点
,点 来确定解析式中的常数
来确定解析式中的常数 ,并且已经求得
,并且已经求得 .
.
(Ⅰ)请你帮老张算出 ,并回答股价什么时候见顶(即求
,并回答股价什么时候见顶(即求 点的横坐标).
点的横坐标).
(Ⅱ)老张如能在今天以 点处的价格买入该股票
点处的价格买入该股票 股,到见顶处
股,到见顶处 点的价格全部卖出,不计其它费用,这次操作他能赚多少元?
点的价格全部卖出,不计其它费用,这次操作他能赚多少元?
甲、乙两人解关于 的方程:
的方程: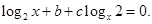 甲写错了常数b,得到根为
甲写错了常数b,得到根为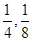 ,乙写错了常数c,得到根为
,乙写错了常数c,得到根为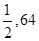 .求方程的真正根。
.求方程的真正根。
已知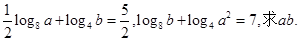
(本小题满分14分)为了解初三学生女生身高情况,某中学对初三女生身高进行了一次抽样调查,根据所得数据整理后列出了频率分布表如下:
组 别频数频率
145.5~149.5 1 0.02
149.5~153.5 4 0.08
153.5~157.5 22 0.44
157.5~161.5 13 0.26
161.5~165.5 8 0.16
165.5~169.5m n
合 计 M N
(1)求出表中所表示的数m,n,M,N分别是多少?
(2)画出频率分布直方图和频率分布折线图.
(3)若要从中再用分层抽样方法抽出10人作进一步调查,则身高在[153.5,161.5)范围内的应抽出多少人?
(4)根据频率分布直方图,分别求出被测女生身高的众数,中位数和平均数?(结果保留一位小数)
(本题满分13分)已知关于x的二次函数
(1)设集合 和
和 ,从集合
,从集合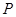 中随机取一个数作为
中随机取一个数作为 ,从
,从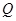 中随机取一个数作为
中随机取一个数作为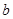 ,求函数
,求函数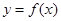 在区间
在区间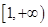 上是增函数的概率;
上是增函数的概率;
(2)设点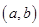 是区域
是区域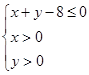 内的随机点,求函数
内的随机点,求函数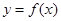 在区间
在区间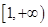 上是增函数的概率.
上是增函数的概率.
(本小题满分14分)
某班甲、乙两名同学参加l00米达标训练,在相同条件下两人l0次训练的成绩(单位:秒)如下:
(I)请画出适当的统计图(茎叶图或频率分布直方图);如果从甲、乙两名同学中选一名参加学校的100米比赛,从成绩的稳定性方面考虑,选派谁参加比赛更好,并说明理由(不用计算,可通过统计图直接回答结论).
(Ⅱ)从甲、乙两人的10次成绩中各随机抽取一次,求抽取的成绩中至少有一个不高于 12.8秒的概率.
(III)经过对甲、乙两位同学的若干次成绩的统计,甲、乙的成绩都均匀分布在[11.5,14.5]之间,
现甲、乙比赛一次,求甲、乙成绩之差的绝对值小于0.8秒的概率.