用密度为 、电阻率为
、电阻率为 、横截面积为
、横截面积为 的薄金属条制成边长为
的薄金属条制成边长为 的闭合正方形框
的闭合正方形框 。如图所示,金属方框水平放在磁极的狭缝间,方框平面与磁场方向平行。设匀强磁场仅存在于相对磁极之间,其它地方的磁场忽略不计。可认为方框的
。如图所示,金属方框水平放在磁极的狭缝间,方框平面与磁场方向平行。设匀强磁场仅存在于相对磁极之间,其它地方的磁场忽略不计。可认为方框的 边和
边和 边都处在磁极之间,极间磁感应强度大小为
边都处在磁极之间,极间磁感应强度大小为 。方框从静止开始释放,其平面在下落过程中保持水平(不计空气阻力)。
。方框从静止开始释放,其平面在下落过程中保持水平(不计空气阻力)。
(1)求方框下落的最大速度 (设磁场区域在数值方向足够长);
(设磁场区域在数值方向足够长);
(2)当方框下落的加速度为 时,求方框的发热功率
时,求方框的发热功率 ;
;
(3)已知方框下落时间为 时,下落高度为
时,下落高度为 ,其速度为
,其速度为 。若在同一时间
。若在同一时间 内,方框内产生的热与一恒定电流
内,方框内产生的热与一恒定电流 在该框内产生的热相同,求恒定电流
在该框内产生的热相同,求恒定电流 的表达式。
的表达式。
一厚度为 的大平板玻璃水平放置,其下表面贴有一半径为 的圆形发光面。在玻璃板上表面放置一半径为 的圆纸片,圆纸片与圆形发光面的中心在同一竖直线上。已知圆纸片恰好能完全挡住从圆形发光面发出的光线(不考虑反射),求平板玻璃的折射率。
如图所示,两气缸
粗细均匀,等高且内壁光滑,其下部由体积可忽略的细管连通;
的直径为
的2倍,
上端封闭,
上端与大气连通;两气缸除
顶部导热外,其余部分均绝热。两气缸中各有一厚度可忽略的绝热轻活塞
,活塞下方充有氮气,活塞
上方充有氧气;当大气压为
,外界和气缸内气体温度均为7
且平衡时,活塞
离气缸顶的距离是气缸高度的
,活塞
在气缸的正中央。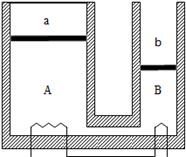
(ⅰ)现通过电阻丝缓慢加热氮气,当活塞
升至顶部时,求氮气的温度;
(ⅱ)继续缓慢加热,使活塞
上升,当活塞
上升的距离是气缸高度的
时,求氧气的压强。
半径分别为
和
的同心圆形导轨固定在同一水平面上,一长为
,质量为
且质量分布均匀的直导体棒
置于圆导轨上面,
的延长线通过圆导轨的中心
,装置的俯视图如图所示;整个装置位于一匀强磁场中,磁感应强度的大小为
,方向竖直向下;在内圆导轨的
点和外圆导轨的
点之间接有一阻值为R的电阻(图中未画出)。直导体棒在水平外力作用下以角速度
绕
逆时针匀速转动,在转动过程中始终与导轨保持良好接触。设导体棒与导轨之间的动摩擦因数为μ,导体棒和导轨的电阻均可忽略,重力加速度大小为
,
求:(1)通过电阻 的感应电流的方向和大小;
(2)外力的功率。
2012年10月,奥地利极限运动员菲利克斯·鲍姆加特纳乘气球升至约
的高空后跳下,经过4分20秒到达距地面约
高度处,打开降落伞并成功落地,打破了跳伞运动的多项世界纪录,取重力加速度的大小
.
(1)忽略空气阻力,求该运动员从静止开始下落到
高度处所需要的时间及其在此处速度的大小.
(2)实际上物体在空气中运动时会受到空气阻力,高速运动受阻力大小可近似表示为
,其中
为速率,
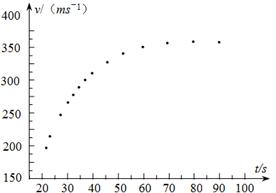
为阻力系数,其数值与物体的形状,横截面积及空气密度有关,已知该运动员在某段时间内高速下落的
图象如图所示,着陆过程中,运动员和所携装备的总质量
,试估算该运动员在达到最大速度时所受阻力的阻力系数(结果保留1位有效数字)。
如图,质量分别为 、 的两个小球 、 静止在地面上方, 球距地面的高度 , 球在 球的正上方。 先将 球释放,经过一段时间后再将 球释放。 当 球下落 时,刚好与 球在地面上方的 点处相碰,碰撞时间极短,碰后瞬间 球的速度恰为零。已知 ,重力加速度大小为 。

(i) 球第一次到达地面时的速度;
(ii) 点距离地面的高度。