设数列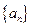 的前
的前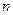 项和为
项和为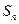 ,点
,点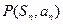 在直线
在直线 上,
上, 为常数,
为常数,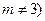 .
.
(Ⅰ)求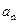 ;
;
(Ⅱ)若数列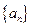 的公比
的公比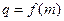 ,数列
,数列 满足
满足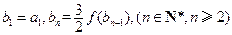 ,求证:
,求证: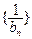 为等差数列,并求
为等差数列,并求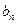 ;
;
(III)设数列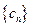 满足
满足 ,
, 为数列
为数列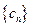 的前
的前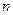 项和,且存在实数
项和,且存在实数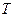 满足
满足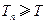 ,
,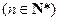 ,求
,求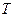 的最大值.
的最大值.
已知命题:末位是0的整数,可以被5整除 .把命题改写为“若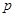 ,则
,则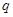 ”的形式,并写出它的逆命题、否命题与逆否命题,并分别判断其真假 .
”的形式,并写出它的逆命题、否命题与逆否命题,并分别判断其真假 .
某食品厂定期购买面粉。已知该厂每天需用面粉6t,每t面粉的价格为1800元,面粉的保管等其他费用为平均每t每天3元,购买面粉每次需支付运费900元. 求该厂多少天购买一次面粉,才能使平均每天所支付的总费用最少?
已知正数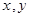 满足
满足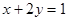 ,求
,求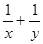 的最小值有如下解法:
的最小值有如下解法:
解:∵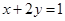 且
且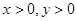 .
.
∴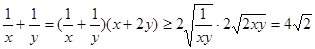
∴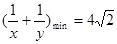 .
.
判断以上解法是否正确?说明理由;若不正确,请给出正确解法.
已知直角△ABC中,周长为L,面积为S,求证:4S≤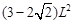 .
.
已知:在 中, ∠A,∠B,∠C, 的对边分别是a, b, c,则求满足下列条件的∠B的范围分别是什么。
中, ∠A,∠B,∠C, 的对边分别是a, b, c,则求满足下列条件的∠B的范围分别是什么。
⑴若 a=2, b=1。⑵若 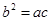 。
。