(本小题满分12分)
某中学共有1000名学生参加了该地区高三第一次质量检测的数学考试,数学成绩如下表所示:
| 数学成绩分组 |
 |
 |
 |
 |
 |
| 人数 |
60 |
90 |
300 |
x |
160 |
(I)为了了解同学们前段复习的得失,以便制定下阶段的复习计划,学校将采用分层抽
样的方法抽取100名同学进行问卷调查,甲同学在本次测试中数学成绩为95分,
求他被抽中的概率;
(II)已知本次数学成绩的优秀线为110分,试根据所提供数据估计该中学达到优秀线的人数;
(III)作出频率分布直方图,并估计该学校本次考试的数学平均分。(同一组中的数据用该组区间的中点值作代表)
设椭圆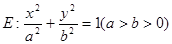 的离心率
的离心率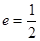 ,
,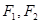 是其左右焦点,点
是其左右焦点,点 是直线
是直线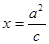 (其中
(其中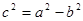 )上一点,且直线
)上一点,且直线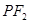 的倾斜角为
的倾斜角为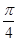 .
.
(Ⅰ)求椭圆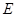 的方程;
的方程;
(Ⅱ)若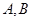 是椭圆
是椭圆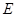 上两点,满足
上两点,满足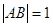 ,求
,求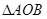 (
(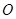 为坐标原点)面积的最小值.
为坐标原点)面积的最小值.
设函数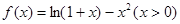 ,数列
,数列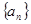 前
前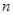 项和
项和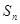 ,
,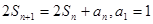 ,数列
,数列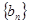 ,满足
,满足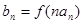 .(Ⅰ)求数列
.(Ⅰ)求数列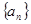 的通项公式
的通项公式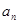 ;
;
(Ⅱ)设数列 的前
的前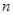 项和为
项和为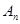 ,数列
,数列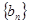 的前
的前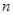 项和为
项和为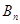 ,证明:
,证明: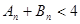 。
。
如图,边长为a的正方形ABCD中,点E、F分别在AB、BC上,且 ,将△AED、△CFD分别沿DE、DF折起,使A、C两点重合于点
,将△AED、△CFD分别沿DE、DF折起,使A、C两点重合于点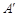 ,连结A¢B.
,连结A¢B.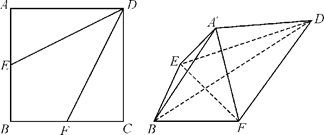
(Ⅰ)判断直线EF与A¢D的位置关系,并说明理由;
(Ⅱ)求二面角F-A¢B-D的大小.
一个口袋中有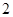 个白球和
个白球和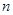 个红球
个红球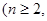 且
且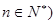 ,每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
,每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
(Ⅰ)试用含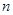 的代数式表示一次摸球中奖的概率
的代数式表示一次摸球中奖的概率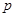 ;
;
(Ⅱ)若 ,求三次摸球恰有一次中奖的概率;
,求三次摸球恰有一次中奖的概率;
(Ⅲ)记三次摸球恰有一次中奖的概率为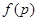 ,当
,当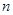 为何值时,
为何值时,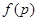 取最大值.
取最大值.
已知向量 ,
, ,
,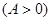 ,函数
,函数 的最大值为
的最大值为 .
.
(Ⅰ)求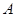 ;
;
(Ⅱ)将函数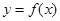 的图像向左平移
的图像向左平移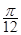 个单位,再将所得图像上各点的横坐标缩短为原来的
个单位,再将所得图像上各点的横坐标缩短为原来的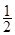 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数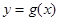 的图像,求
的图像,求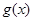 在
在 上的值域.
上的值域.