(本小题共16分)
已知椭圆 和圆
和圆 :
: ,过椭圆上一点
,过椭圆上一点 引圆
引圆 的两条切线,切点分别为
的两条切线,切点分别为 . (1)①若圆
. (1)①若圆 过椭圆的两个焦点,求椭圆的离心率
过椭圆的两个焦点,求椭圆的离心率 ; ②若椭圆上存在点
; ②若椭圆上存在点 ,使得
,使得 ,求椭圆离心率
,求椭圆离心率 的取值(2)设直线
的取值(2)设直线 与
与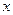 轴、
轴、 轴分别交于点
轴分别交于点 ,
,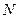 ,求证:
,求证: 为定值.
为定值.
(本小题满分12分)
如图,在四棱锥P—ABCD中,底面ABCD是矩形,已知AB = 3,AD = 2,PA = 2,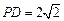 ,
, .
.
(1)证明:AD⊥平面PAB;
(2)求异面直线PC与AD所成的角的大小;
(3)求二面角P—BD—A的大小.
(本小题满分13分)
已知函数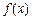 的导数
的导数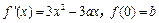 .a,b为实数,
.a,b为实数,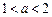 .
.
(1)若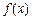 在区间
在区间 上的最小值、最大值分别为
上的最小值、最大值分别为 、1,求a、b的值;
、1,求a、b的值;
(2)在 (1) 的条件下,求曲线在点P(2,1)处的切线方程.
(本小题满分13分)
有A、B、C、D、E共5个口袋,每个口袋装有大小和质量均相同的4个红球和2个黑球,现每次从其中一个口袋中摸出3个球,规定:若摸出的3个球恰为2个红球和1个黑球,则称为最佳摸球组合.
(1)求从口袋A中摸出的3个球为最佳摸球组合的概率;
(2)现从每个口袋中摸出3个球,求恰有3个口袋中摸出的球是最佳摸球组合的概率.
(本小题满分13分)
已知函数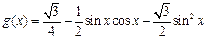 的图象按向量
的图象按向量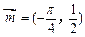 平移得到函数
平移得到函数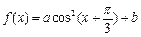 的图象.
的图象.
(1)求实数a、b的值;
(2)设函数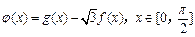 ,求函数
,求函数 的单调递增区间和最值.
的单调递增区间和最值.
(本小题满分12分)
数列 :满足
:满足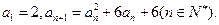
(1)设 ,求证
,求证 是等比数列;
是等比数列;
(2)求数列 的通项公式;
的通项公式;
(3)设 ,数列
,数列 的前
的前 项和为
项和为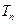 ,求证:
,求证: