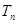(本小题共16分)
已知数列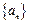 各项均不为0,其前
各项均不为0,其前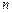 项和为
项和为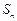 ,且对任意
,且对任意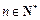 都有
都有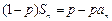 (
(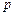 为大于1的常数),记f(n)
为大于1的常数),记f(n)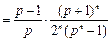 .
.
(1)求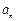 ;
;
(2)试比较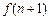 与
与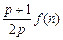 的大小(
的大小(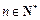 );
);
(3)求证:(2n-1)f(n)≤f(1)+f(2)+…+f(2n-1) ≤[1-()2n-1] (n∈N*)
(本小题满分14分)如图1,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,D为侧棱PC上一点,它的正(主)视图和侧(左)视图如图2所示.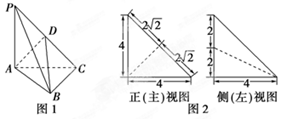
(1)证明:AD⊥平面PBC;
(2)求三棱锥D-ABC的体积;
(本小题满分14分)函数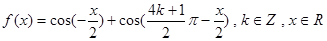 。
。
(1)求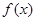 的周期;(2)
的周期;(2)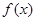 在
在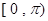 上的减区间;
上的减区间;
(3)若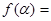
 ,
, ,求
,求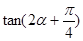 的值。
的值。
(本小题满分12分)如图,函数y=2sin( x+φ) x∈R , 其中0≤φ≤
x+φ) x∈R , 其中0≤φ≤ 的图象与y轴交于点(0,1).
的图象与y轴交于点(0,1).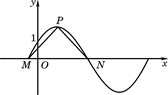
(Ⅰ)求φ的值;
(Ⅱ)设P是图象上的最高点,M、N是图象与x轴的交点,求
(本小题满分12分)已知函数 ,
,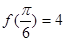 ,
,
(1)求实数a的值;(2)求函数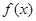 在
在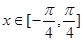 的值域。
的值域。
设数列 为等差数列,且
为等差数列,且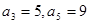 ;数列
;数列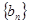 的前n项和为
的前n项和为 ,且
,且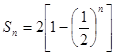 .
.
(Ⅰ)求数列 ,
,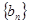 的通项公式;
的通项公式;
(Ⅱ)若 ,
,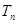 为数列
为数列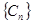 的前n项和,求
的前n项和,求