((本小题满分12分)在直三棱柱ABC—A1B1C1中,CA=CB=CC1=2, ,E、F分别是BA、BC的中点,G是AA1上一点,且
,E、F分别是BA、BC的中点,G是AA1上一点,且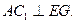
(Ⅰ)确定点G的位置;
(Ⅱ)求三棱锥C1—EFG的体积. 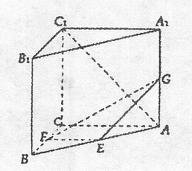
已知首项为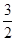 的等比数列
的等比数列 不是递减数列,其前n项和为
不是递减数列,其前n项和为 ,且
,且 成等差数列。
成等差数列。
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列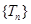 的最大项的值与最小项的值。
的最大项的值与最小项的值。
某产品具有一定的时效性,在这个时效期内,由市场调查可知,在不做广告宣传且每件获利a元的前提下,可卖出b件;若做广告宣传,广告费为n千元比广告费为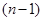 千元时多卖出
千元时多卖出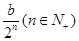 件。
件。
(1)试写出销售量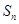 与n的函数关系式;
与n的函数关系式;
(2)当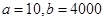 时,厂家应该生产多少件产品,做几千元的广告,才能获利最大?
时,厂家应该生产多少件产品,做几千元的广告,才能获利最大?
设等差数列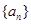 满足
满足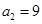 ,且
,且 是方程
是方程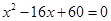 的两根。
的两根。
(1)求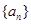 的通项公式;(2)求数列
的通项公式;(2)求数列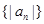 的前n项和
的前n项和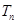 。
。
吉安一中新校区正在如火如荼地建设中,如图,某工地的平面图呈圆心角为120°的扇形AOB,工地的两个出入口设置在点A及点C处,工地中有两条笔直的小路AD、DC,长度分别为300米、500米,且DC平行于OB。求该扇形的半径OA的长(精确到1米)。
在△ABC中,角A,B,C的对边分别为 ,且
,且 。
。
(1)求 的值;(2)求c的值。
的值;(2)求c的值。