（（本小题满分14分）
如图：设工地有一个吊臂长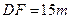
的吊车，吊车底座
高
，现准备把一个底半径为
高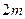
的圆柱形工件吊起平放到
高的桥墩上，问能否将工件吊到桥墩上？（参考数据：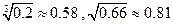
）
已知函数
, 
.
（Ⅰ）当
时，求曲线
在点
处的切线方程；
（Ⅱ）当
时，求函数
的单调区间；
（Ⅲ）当
时，函数在
上的最大值为
，若存在
，使得
成立，求实数b的取值范围.
如图，四边形
与
都是边长为
的正方形，点E是
的中点，
求证：
；
求证：平面
；
求体积
与
的比值。
某商场销售某种商品的经验表明，该商品每日的销售量y（单位：千克）与销售价格x （单位：元/千克）满足关系式y=
+10(x-6)2，（其中3<x<6，
为常数，）已知销售价格为5元/千克时，每日可售出该商品11千克。
(I）求的值；
(II）若该商品的成品为3元/千克，试确定销售价格x的值，使商场每日销售该商品所获得的利润最大。
设命题
：
，命题
：
；
如果“或”为真，“且”为假，求
的取值范围。
已知焦距为
的双曲线的焦点在x轴上，且过点P
.
（Ⅰ）求该双曲线方程；
（Ⅱ）若直线m经过该双曲线的右焦点且斜率为1，求直线m被双曲线截得的弦长.