本题满分14分)
为了解高中一年级学生身高情况,某校按10%的比例对全校700名高中一年级学生按性别进行抽样检查,测得身高频数分布表如下表1、表2.
表1:男 生身高频数分布表
生身高频数分布表
表2:女生身高频数分布表
(1)求该校男生的人数并完成下面频率分布直方图;
(2)估计该校学生身高(单位:cm)在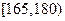 的概率;
的概率;
(3)在男生样本中,从身高(单位:cm)在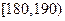 的男生中任选3人,设
的男生中任选3人,设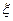 表示所选3人中身高(单位:cm)在
表示所选3人中身高(单位:cm)在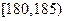 的人数,求
的人数,求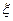 的分布列和数学期望.
的分布列和数学期望.
(本小题满分14分)已知数列 的前
的前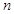 项和为
项和为 ,点
,点 在直线
在直线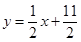 上;数列
上;数列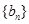 满足
满足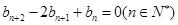 ,且
,且 ,它的前9项和为153.
,它的前9项和为153.
(1)求数列 、
、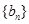 的通项公式;
的通项公式;
(2)设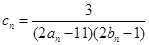 ,数列
,数列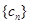 的前
的前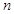 项和为
项和为 ,求使不等式
,求使不等式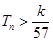 对一切
对一切 都成立的最大正整数
都成立的最大正整数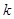 的值;
的值;
(3)设 ,是否存在
,是否存在 ,使得
,使得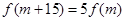 成立?若存在,求出
成立?若存在,求出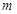 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本小题满分14分)
设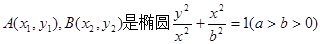 上的两点,
上的两点,
满足 ,椭圆的离心率
,椭圆的离心率 短轴长为2,0为坐标原点.
短轴长为2,0为坐标原点.
(1)求椭圆的方程;
(2)试问:△AOB的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
(本小题满分14分)已知如图(1),梯形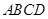 中,
中, ,
,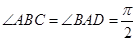 ,
, ,
, 、
、 分别是
分别是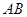 、
、 上的动点,且
上的动点,且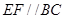 ,设
,设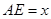 (
(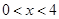 )。沿
)。沿 将梯形
将梯形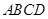 翻折,使平面
翻折,使平面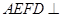 平面
平面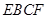 ,如图(2)。
,如图(2)。
(Ⅰ)求证:平面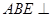 平面
平面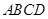 ;
;
(Ⅱ)若以 、
、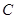 、
、 、
、 为顶点的三棱锥的体积记为
为顶点的三棱锥的体积记为 ,求
,求 的最大值;
的最大值;
(Ⅲ)当 取得最大值时,求二面角
取得最大值时,求二面角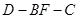 的正弦值.
的正弦值.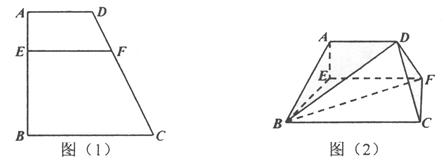
(本小题满分14分)已知函数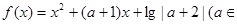 R,且
R,且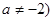 .
.
(I)若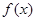 能表示成一个奇函数
能表示成一个奇函数 和一个偶函数
和一个偶函数 的和,求
的和,求 的解析式;
的解析式;
(II)命题P:函数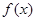 在区间
在区间 上是增函数;
上是增函数;
命题Q:函数 是减函数.
是减函数.
如果命题P、Q有且仅有一个是真命题,求a的取值范围;
.(本小题满分12分)口袋中有质地、大小完全相同的5个球,编号分别为1,2,3,4,5,甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.
(Ⅰ)求甲赢且编号的和为6的事件发生的概率;
(Ⅱ)这种游戏规则公平吗?试说明理由.