(文科做以下(1)(2)(3))
(1)、已知 ,求数列
,求数列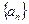 的通项公式;
的通项公式;
(2)、在(1)的条件下,数列 ,求证数列
,求证数列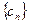 是一个 “1类和科比数列”;
是一个 “1类和科比数列”;
(3)、设等差数列 是一个 “
是一个 “ 类和科比数列”,其中首项
类和科比数列”,其中首项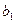 ,公差
,公差 ,探究
,探究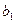
与 的数量关系,并写出相应的常数
的数量关系,并写出相应的常数 ;
;
【改编】(本小题满分14分)已知函数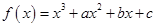 .
.
(1)当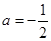 ,
,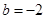 时,求函数
时,求函数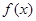 的极值;
的极值;
(2)若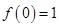 ,且对
,且对 ,不等式
,不等式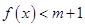 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(本小题满分14分)设抛物线的顶点在坐标原点,焦点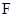 在
在 轴正半轴上,过点
轴正半轴上,过点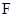 的直线交
的直线交
抛物线于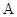 ,
,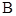 两点,线段
两点,线段 的长是
的长是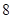 ,
, 的中点到
的中点到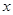 轴的距离是
轴的距离是 .
.
(1)求抛物线的标准方程;
(2)在抛物线上是否存在不与原点重合的点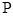 ,使得过点
,使得过点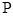 的直线交抛物线于另一点
的直线交抛物线于另一点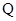 ,满足
,满足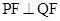 ,
,
且直线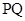 与抛物线在点
与抛物线在点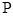 处的切线垂直?若存在,求出点
处的切线垂直?若存在,求出点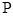 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(本小题满分14分)数列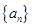 (
( )的前
)的前 项和
项和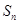 满足
满足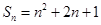 .
.
(1)求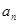 ;
;
(2)若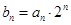 ,设数列
,设数列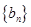 的前
的前 项和为
项和为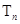 ,求
,求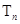 .
.
(本小题满分14分)如图,直三棱柱 中,
中,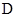 ,
,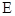 分别是
分别是 ,
,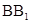 的中点.
的中点.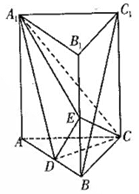
(1)证明: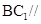 平面
平面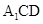 ;
;
(2)设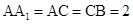 ,
,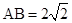 ,求三棱锥
,求三棱锥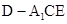 的体积.
的体积.
(本小题满分12分)以下茎叶图记录了甲、乙两组各三名同学在期末考试中的数学成绩.乙组
记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中以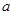 表示.
表示. 
(1)若甲、乙两个小组的数学平均成绩相同,求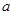 的值;
的值;
(2)求乙组平均成绩超过甲组平均成绩的概率.