设函数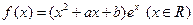 .
.
(1)若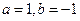 ,求函数
,求函数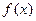 的极值;
的极值;
(2)若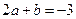 ,试确定
,试确定 的单调性;
的单调性;
(3)记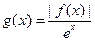 ,且
,且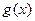 在
在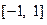 上的最大值为M,证明:
上的最大值为M,证明: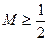 .
.
设 ,其中
(Ⅰ)求函数
的值域;
(Ⅱ)若
在
 上为增函数,求
的最大值
甲、乙两人轮流投篮,每人每次投一票.约定甲先投中者获胜,一直到有人获胜或每人都已投球3次时投篮结束.设甲每次投篮投中的概率为 ,乙每次投篮投中的概率为 ,且各次投篮互不影响.
(Ⅰ) 求甲获胜的概率;
(Ⅱ)求投篮结束时甲的投篮次数 的分布列与期望
设函数
,其中在
,曲线
在点
处的切线垂直于
轴
(Ⅰ)求
的值;
(Ⅱ)求函数
极值.
已知函数
(
为常数,
是自然对数的底数),曲线
在点
处的切线与
轴平行.
(Ⅰ)求
的值;
(Ⅱ)求
的单调区间;
(Ⅲ)设
,其中
为
的导函数.证明:对任意
.
在平面直角坐标系
中,
是抛物线
的焦点,
是抛物线
上位于第一象限内的任意一点,过
三点的圆的圆心为
,点
到抛物线
的准线的距离为
.
(Ⅰ)求抛物线
的方程;
(Ⅱ)是否存在点
,使得直线
与抛物线
相切于点
?若存在,求出点
的坐标;若不存在,说明理由;
(Ⅲ)若点
的横坐标为
,直线
与抛物线
有两个不同的交点
,
与圆
有两个不同的交点
,求当
时,
的最小值.