(本小题12分)
如图所示,已知圆 为圆上一动点,点
为圆上一动点,点 在
在 上,点
上,点 在
在 上,且满足
上,且满足 的轨迹为曲线
的轨迹为曲线 .
.
(I)求曲线 的方程;
的方程;
(II)若过定点F(0,2)的直线交曲线 于不同的
于不同的 两点
两点 (点
(点 在点
在点 之间),且满足
之间),且满足 ,求
,求 的取值范围.
的取值范围.
(满分14分)设函数 的定义域是R,对于任意实数
的定义域是R,对于任意实数 ,恒有
,恒有 ,且当
,且当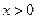 时,
时,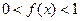 。
。
⑴求证: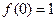 ,且当
,且当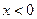 时,有
时,有 ;
;
⑵判断 在R上的单调性;
在R上的单调性;
⑶设集合 ,集合
,集合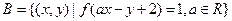 ,若A∩B=
,若A∩B= ,求a的取值范围。
,求a的取值范围。
(满分14分)已知二次函数f(x)的二次项系数为a,且不等式f(x)>-2x的解集为(1,3).
(1)若方程f(x)+6a=0有两个相等的根,求f(x)的解析式;
(2)若f(x)的最大值为正数,求实数a的取值范围.
(满分14分)已知动圆经过点(1,0),且与直线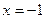 相切,
相切,
(1)求动圆圆心的轨迹方程。
(2)在(1)中的曲线上求一点,使这点到直线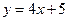 的距离最短。
的距离最短。
(满分12分)已知集合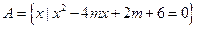 ,
,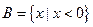 ,若
,若 ,求实数
,求实数 的取值范围。
的取值范围。
(满分12分)已知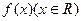 恒不为0,对于任意
恒不为0,对于任意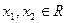
等式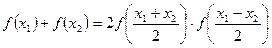 恒成立.求证:
恒成立.求证: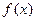 是偶函数.
是偶函数.