(本小题满分8分)下面三条直线l1:4x+y=4,l2:mx+y=0,l3:2x-3my=4不能构成三角形.求m的取值范围.
(本大题14分)已知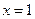 是函数
是函数 的一个极值点,其中
的一个极值点,其中 ,
,
(I)求 与
与 的关系式;
的关系式;
(II)求 的单调区间;
的单调区间;
(III)当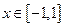 时,函数
时,函数 的图象上任意一点的切线斜率恒大于3
的图象上任意一点的切线斜率恒大于3 ,求
,求 的取值范围.
的取值范围.
(本大题12分)定义在R上的单调函数 满足
满足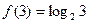 且对任意
且对任意 都有
都有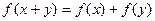 .
.
(1)求证 为奇函数;
为奇函数;
(2)若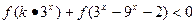 对任意
对任意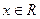 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
(本大题12分)
为了迎接2010年10月1日国庆节,某城市为举办的大型庆典活动准备了四种保证安全的方案,列表如下:
| 方案 |
A |
B |
C |
D |
| 经费 |
300万元 |
400万元 |
500万元 |
600万元 |
| 安全系数 |
0.6 |
0.7 |
0.8 |
0.9 |
其中安全系数表示实施此方案能保证安全的系数,每种方案相互独立,每种方案既可独立用,又可以与其它方案合用,合用时,至少有一种方案就能保证整个活动的安全
(I)求A、B两种方案合用,能保证安全的概率;
(II)若总经费在1200万元内(含1200万元),如何组合实施方案可以使安全系数最高?
(本小题满分12分)
如图,在四棱锥P-ABCD中,底面ABCD是矩形,M、N分别为PA、BC的中点,PD⊥平面ABCD,且PD=AD= ,CD=1
,CD=1
(1)证明:MN∥平面PCD;
(2)证明:MC⊥BD;
(3)求二面角A—PB—D的余弦值。
(本大题12分)设 :实数
:实数 满足
满足 ,其中
,其中 ,命题
,命题 实数
实数 满足
满足 .
.
(Ⅰ)若 且
且 为真,求实数
为真,求实数 的取值范围;
的取值范围;
(Ⅱ)若 是
是
 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围.
的取值范围.