(本小题满分12分)将编号为1,2,3,4的四张同样材质的卡片,随机放入编码分别为1,2,3,4的四个小盒中,每盒仅放一张卡片,若第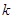 号卡片恰好落入第
号卡片恰好落入第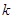 号小盒中,则称其为一个匹对,用
号小盒中,则称其为一个匹对,用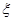 表示匹对的个数.
表示匹对的个数.
(1)求第2号卡片恰好落入第2号小盒内的概率;
(2)求匹对数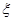 的分布列和数学期望
的分布列和数学期望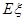 .
.
已知锐角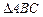 中,三个内角为A、B、C,两向量
中,三个内角为A、B、C,两向量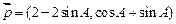 ,
,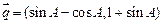 。若
。若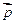 与
与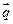 是共线向量.
是共线向量.
(I)求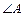 的大小;(II)求函数
的大小;(II)求函数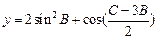 取最大值时,
取最大值时,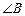 的大小.
的大小.
(本小题满分14分)定义在D上的函数 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数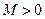 ,都有
,都有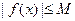 成立,则称
成立,则称 是D上的有界函数,其中M称为函数
是D上的有界函数,其中M称为函数 的上界。已知函数
的上界。已知函数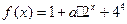 ,
,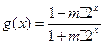 当
当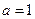 时,求函数
时,求函数 在
在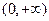 上的值域,并判断函数
上的值域,并判断函数 在
在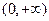 上是否为有界函数,请说明理由;若函数
上是否为有界函数,请说明理由;若函数 在
在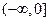 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数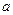 的取值范围;若
的取值范围;若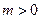 ,求函数
,求函数 在
在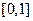 上的上界T的取值范围。
上的上界T的取值范围。
(本小题满分12分)
设函数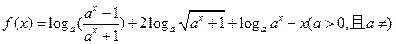 化简函数式并求函数
化简函数式并求函数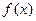 的定义域;解不等式
的定义域;解不等式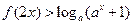
(本小题满分12分)已知集合 ,集合
,集合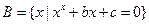 ,且
,且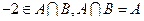 ,求实数
,求实数 的值。
的值。
(本小题满分12分)已知函数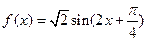
若将函数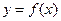 的图像向左平移
的图像向左平移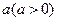 个单位长度得到的图像恰好关于点
个单位长度得到的图像恰好关于点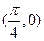 对称,求实数
对称,求实数 的最小值;若函数
的最小值;若函数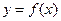 在
在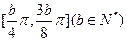 上为减函数,试求实数b的值。
上为减函数,试求实数b的值。